Les figures de l’Intuition
MODELISATION GEOMETRIQUE DE QUELQUES TYPES DE RAISONNEMENTS
Les « figures de l’intuition »

PROJET PERSONNALISE : M. BOUSQUET PHILIPPE
ENSEIGNANT RESPONSABLE : Mme JALLEY
Ecole Centrale Paris, 1981
![]()
INTRODUCTION
« Des intuitions sans concepts sont aveugles, mais des concepts sans intuitions sont vides. »
Kant.
« Les images se précipitaient, des tours, des cercles les uns sur les autres, un cylindre placé en oblique. Tout est en mouvement, en croissance; les tours s’élèvent de plus en plus, le cercle se creuse et devient cylindre… ». Telles sont les impressions décrites par un patient du psychologue Kretschmer à la lecture d’un passage de Kant sur la question de l’infini sans l’espace[1].Cette floraison déconcertante de figures géométriques, dont les transformations épousent par une nécessité quasi mécanique le développement d’un raisonnement abstrait, relève certes de la pathologie. Mais ne peut-on y voir l’expression exacerbée d’une faculté générale de l’esprit, qui lui permet de se forger des représentations imagées comme support d’un raisonnement, faculté dont l’importance et la presque universalité sont avérées par de nombreux témoignages ?
J.Hadamard, dans son « Essai sur la psychologie de l’invention dans les domaines mathématiques » a rassemblé ceux des principaux créateurs scientifiques de son temps. Le témoignage d’Einstein est justement célèbre : « les mots et le langage, écrits ou parlés, ne semblent pas jouer le moindre rôle dans le mécanisme de ma pensée. Les entités psychiques qui servent d’éléments à la pensée sont certains signes ou des images plus ou moins claires, qui peuvent « à volonté » être reproduits et combinés… » Pour Hadamard lui-même : « 1’aide des images est absolument nécessaire à la conduite de ma pensée, et je ne suis jamais trompé par elles« . Cependant, l’entreprise que s’est fixée ce mathématicien d’étudier les conditions de la création scientifique ressemble fort à une gageure : si elle apporte aux tenants de la pensée non verbale une confirmation essentielle -Schopenhauer n’allait-il pas jusqu’à dire que « les pensées meurent au moment où elles s’incarnent dans les mots »-, elle n’en reste pas moins extrêmement vague sur ce que sont effectivement ces « images » que manipulent si spontanément et si efficacement, à les croire, les savants les plus austères : « le jeu sur les éléments mentionnés vise à être analogue à certaines connexions logiques que l’on recherche… », il semble qu’on ne puisse guère aller plus loin que cette constatation d’Einstein.
Un des rares cas précis cité par Hadamard est celui de sa « vision » personnelle de la démonstration selon laquelle il existe, par exemple, un nombre premier supérieur à 11 :
|
|
|
|
|
|
|
|
On voit que les images manipulées sont extrêmement élémentaires (amas, points) et que leur mode de signification est basé principalement sur les rapports spatiaux qu’elles entretiennent entre elles, dans un espace intuitif propre à leur créateur. Il semble bien en tout cas qu’il ne s’agisse nullement de perceptions visuelles rémanentes, sinon de manière très lointaine, mais plutôt de schémas abstraits utilisant des éléments géométriques simples, créations instantanées en réponse à un problème précis, ou produits durables de l’élaboration raisonnée d’un « dictionnaire » personnel.
Dans la mesure où, comme le pense Hadamard, « donner de la précision à ces images risquerait de les altérer », la tentative de cet auteur n’en apparaît que plus méritoire; car, bien que cette imagerie mentale constitue sans doute un des fondements essentiels de la création scientifique, elle représente cependant, du fait de son flou nécessaire, de son caractère difficilement communicable à qui n’en a pas l’expérience personnelle, l’opposé d’un objet d’étude scientifique.
Rien d’étonnant donc à ce que les ouvrages achevés, du moins dans leur grande majorité, manifestent une remarquable pudeur à l’égard de leurs sources intuitives (ainsi par exemple les puissantes analogies hydrodynamiques qui ont fourni à Maxwell sa « vision » de l’électromagnétisme, disparaissent entre les travaux préparatoires et le mémoire définitif), ceci d’une manière certes assez légitime (puisque toute formalisation véritable, toute axiomatisation, passe par l’épuration totale de ces résidus intuitifs, foyers d’imprécision et d’erreurs)- mais néanmoins dommageable à une étude épistémologique : les témoignages directs sur les sources d’inspiration des savants sont rares, extérieurs le plus souvent à leur oeuvre scientifique. A.Koestler en a rassemblé quelques-uns dans son livre consacré à la création, « Le cri d’Archimède », qui conclut qu’on a certainement surestimé, depuis le siècle des Lumières, le rôle des processus strictement intellectuels pour la pensée scientifique, au détriment d’une puissance visionnaire pré-verbale commune à tous les grands créateurs.
En résumé, il semble prouvé que des images mentales proches de figures géométriques simples jouent un rôle important dans la pensée scientifique, tant au niveau de la recherche intuitive qui précède l’émergence d’une notion, que dans la conduite même d’un raisonnement. Comme cependant ces images ne sont aucunement nécessaires – voire même nuisibles – à l’expression de la pensée achevée, une étude directe, du type de celle d’Hadamard, semble extrêmement difficile puisqu’elle suppose, envers les notions figurées, le même genre d’intimité que celle de leur créateur.
Cependant, puisque ces images sont liées à une étape de construction des concepts, il semble logique, transposant le problème dans une perspective historique, de rechercher dans les époques pré-scientifiques un matériau plus accessible. Là, dans une pensée qui demeure très souvent métaphorique et analogique, où le raisonnement, faute de formalisation et de mathématisation, émerge à peine du royaume de la suggestion liée aux mots et aux images, il est possible d’observer le recours sans frein à cette faculté imageante. Désireux de nous éloigner le moins possible de la pensée scientifique, nous n’avons pas exploré les domaines spécifiques du mythe et de l’imaginaire, où pourtant on retrouverait sans doute – mais inextricablement liées à des figures plus complexes -, des intuitions géométriques. Nous avons interrogé seulement les auteurs qui, suivant les moyens et les illusions de leur temps, ont recherché la rigueur de la Raison, philosophes et savants dont les conceptions se préfigurent et s’influencent mutuellement, dont les intuitions se ressemblent, si différentes que soient les oeuvres achevées.
Ce présupposé d’une unité profonde des intuitions de base et des processus créatifs doit être considéré comme une hypothèse de travail, sans laquelle cette étude.comparée des principales « figures » intuitives n’aurait aucun sens. Nous n’avons pas cherché à vérifier cette hypothèse, à analyser le détail de ces processus psychologiques : mais seulement à constituer, au travers d’exemples nombreux, un répertoire de quelques unes de ces formes intermédiaires, de ces « signes, soutiens de la pensée intuitive » dont R.Jakobson, dans une lettre à Hadamard, propose la classification suivantes : signes conventionnels d’une part, propres à une société et signes personnels d’autre part, forgés par le seul individu ; parmi ces derniers, certains, épisodiques, correspondent à un acte créateur particulier ; d’autres au contraire semblent constituer un patrimoine commun à plusieurs créateurs, relativement indépendant des circonstances sociales et historiques : ce sont ces formes « stables » de la pensée intuitive que nous avons essayé de repérer et de classer.
Une telle démarche est nécessairement très apriorique :
- a priori dans le choix de ces formes, puisqu’il ne saurait être question de prétendre à l’exhaustivité. Nous avons retenu celles qui nous semblaient les plus générales, les plus fréquentes, susceptibles d’une traduction en termes géométriques, ou tout au moins de localisation spatiale ; celles, enfin, qui personnellement nous parlaient.
- a priori dans leur classement, que nous avons pu cru pouvoir faire dépendre du nombre d’objets symbolisés, du nombre d' »actants » en présence.
Ceci nous a conduit, afin de simplifier le langage, à utiliser des formulations telles que « la coupure du cercle figure le passage de l’unitarité à la binarité », sans qu’il faille entendre par ces termes de quelconques essences de l’Un ou du Deux aptes à des transformations mystérieuses : nous avons/simplement voulu rendre compte de certains glissements privilégiés entre figures, certains tombant sous le sens, d’autres, plus subtils, traduisant la mobilité de la pensée intuitive.
- a priori dans les rapprochements que nous avons essayé d’établir entre des figures dégagées par l’étude de raisonnements préscientifiques ou philosophiques, et leurs correspondants supposés dans les domaines scientifiques : étant entendu que la démarche inverse, bien plus difficile, serait sans doute plus fructueuse ; des figures spécifiques à la pensée scientifique nous ont ainsi échappé, et nous avons privilégié par contre des formes (par exemple l’opposition des contraires) qui y sont relativement secondaires.
- a priori enfin dans l’abstraction faite de toute référence historique ; nous avons présenté ses formes hors contexte, désincarnées de leur substrat culturel ; nous avons négligé leurs influences mutuelles et leurs évolutions respectives, comme si elles étaient entièrement non-apprises, et réinventées suivant les besoins de chaque créateur.
Cette approximation parait relativement justifiée, par le fait que leur simplicité, leur caractère immédiat, permet à chacun de les extraire de son propre fonds. De plus, la grande extension de leurs emplois, qui résulte de cette simplicité même, rend très difficile le suivi historique de l’une d’entre elles[2].
Nous ne nous dissimulons pas que ces a priori font planer une certaine ambiguïté sur la nature des formes répertoriées : si elles ont certainement quelque analogie avec les images mentales mises en évidence par Hadamard, on ne peut les identifier à elles : en tant que commun dénominateur de pensées créatrices diverses, elles sont en effet trop élémentaires pour se prêter commodément à la représentation de raisonnements élaborés, comme le montrera l’exemple du raisonnement dit « de la diagonale ».
D’autre part, elles ne sont pas réellement homogènes : certaines semblent si profondément enracinées dans les mécanismes de la pensée opératoire et dans la substance même du langage qu’elles ressortissent plutôt d’une étude psychologique et linguistique ; d’autres, qui renvoient à des notions aussi vastes que celles de séparation, d’altérité, de contrariété ou d’unité, relèvent de la philosophie ; d’autres encore, qui confinent à la métaphore, plutôt d’une critique littéraire ; d’autres enfin, restées très proches des objets qu’elles modélisent, d’une critique purement scientifique.
Ces quatre approches possibles, dont parfois toutes sont nécessaires, nous semblent grosso modo être celles des quatre auteurs chez qui nous avons principalement puisé, nous contentant de confronter leurs points de vue :
- L’oeuvre de J.Piaget éclaire d’une lumière nouvelle les rapports du logique et du psychologique : la « psychologie génétique » compare la construction et l’évolution des structures de la personnalité et des structures de la Raison, et 1′ »épistémologie génétique » nous montre comment, dans certains cas, les stades de la connaissance scientifique récapitulent ceux de l’acquisition des connaissances par l’individu. Elle fournit donc un cadre remarquable pour la compréhension de ces images mentales qui, jaillies de l’esprit créateur d’un seul, semblent souvent presque universelles.
- La « Philosophie des formes symboliques » d’E.Cassirer vise à « élargir le projet épistémologique » : « au lieu de se borner à rechercher a sous quelles conditions générales l’homme peut connaître le monde, il devient nécessaire de délimiter mutuellement les principales formes suivant lesquelles il peut le comprendre… ».[3]Le tome I de cet ouvrage étudie dans quelle mesure le langage est dépendant de ces formes, le tome 2 (que nous n’avons pas utilisé) tente de les retrouver dans le mythe, le tome 3 les décèle au sein des concepts scientifiques. On trouve dans ce dernier tome des indications précieuses sur la « fonction symbolisante », bien que les » formes symboliques » étudiées ne soient pas à proprement parler des figurations géométriques (excepté le point fixe), mais des catégories très générales comme l’espace et le temps.
- Chez M.Serres, les formes géométriques deviennent véritablement un objet principal d’étude, passant même avant les notions symbolisées. Ainsi, la « Naissance de la physique dans le texte de Lucrèce » est un essai sur la figure dynamique du tourbillon, de la spirale et de l’écart angulaire. Nous étant limité dès le départ à des figures « statiques », qui représentent un état et non un processus, nous avons surtout utilisé Le Système de Leibniz et ses modèles mathématiques, dont les analyses sur les figures du réseau, de l’étoile et du point ont valeur très générale. M.Serres y déplore incidemment la « pitoyable pauvreté de nos modèles de pensée » : « alors que la science met en évidence des structures ultra-fines, nous philosophons toujours à l’aide de modèles ou de schémas non affinés, au moyen de techniques de raisonnement qui, elles, n’ont guère fait de progrès » [4](4).
- Nous avons trouvé dans le court ouvrage de R. Thom, « Morphogénèse et imaginaire », comme une réponse à cette attente. La « théorie des catastrophes » représente une reconnaissance du rôle de l’analogie dans les sciences, puisqu’elle permet une « classification des « logoi archétypes », c’est-à-dire de tous les types possibles de situations analogiques », la validité de cette réduction reposant sur le fait que « 1’esprit et le monde extérieur possèdent les mêmes mécanismes de régulation et de simulation ». Quoiqu’il en soit, la collection des « catastrophes élémentaires » et des figures obtenues à partir d’elles fournit un riche dictionnaire analogique – parfois assez hermétiqu e- qui permettra peut-être, à terme, de renouveler le sempiternel symbolisme des cercles, des droites et des plans.
Citons enfin, dans les domaines de la Poétique et de l’Imaginaire, les oeuvres de G.Durand et de G.Bachelard, qui mettent en évidence des figures analogues; ainsi notamment dans « La poétique de l’espace », les chapitres sur la phénoménologie du rond, la dialectique du dehors et du dedans, la miniature.
Il est temps désormais de débroussailler quelque peu notre terminologie : nous n’étudions pas les images mentales en général, qui peuvent être aussi bien des souvenirs visuels que des schémas construits, et dont certains psychologues[5] ont pensé qu’elles constituaient l’intégralité du fonctionnement cérébral ; mais seulement celles qui semblent exprimables par des formes géométriques simples. Cependant, nous ne les étudions pas en tant que schémas achevés, tels qu’on peut les trouver en marge d’un livre de géométrie, et qui illustrent des raisonnements particuliers. Il s’agit plutôt de formes préalables ou contemporaines au raisonnement, qui sont comme autant de clés intuitives à essayer successivement, puis à affiner peu à peu, et qui servent, non à calculer, mais à visualiser des relations entre éléments, ainsi que le conseille Descartes[6] « L’imagination sera surtout d’un grand usage lorsqu’il s’agira de résoudre un problème non plus par simple déduction, mais par plusieurs déductions sans liens entre elles, dont il faudra ensuite coordonner les résultats après en avoir fait une énumération complète… Nous risquerions d’ oublier des données si nous n’avions pas sans cesse présente à l’esprit l’image de l’objet sur lequel nous raisonnons, qui nous les représente toutes à chaque instant »
A l’aboutissement de ce processus d’adéquation progressive de la représentation à l’objet, se constitue un modèle, qui rassemble et synthétise les différentes propriétés du substrat (« modèle » atomique de Rutherford par exemple). Bien qu’on puisse retrouver dans le modèle telle ou telle des intuitions primitives qui ont servi à son établissement, leurs caractéristiques individuelles s’effacent devant leur rôle nouveau au sein de l’ensemble, qui seul importe. A l’opposé, la métaphore, cette condensation analogique instantanée de deux choses en une, ne vise le plus souvent qu’une seule caractéristique de la figure : le cercle par exemple, figure « sans commencement ni fin », comme métaphore de l’éternité.
La notion que nous essayons de dégager se situe à mi-chemin de ces deux pôles : plus riche que la métaphore, puisque se prêtant le plus souvent à diverses interprétations, mais moins complète que le modèle, qui fige définitivement un grand nombre de rapports, nous avons cru bon de la dénommer « figure de l’intuition », afin de rappeler qu’elle participe à la fois, par sa nature de la « figure géométrique », et par son imprécision nécessaire de la « figure de style ».
Entre l’analyse de l’extension, des propriétés symboliques et des transformations de ces « figures » , et la simple constatation de leur puissance persuasive, nous avons essayé d’ébaucher au mieux une topologie, au pire une rhétorique.
![]()
LA FRONTIERE
« Cela pense, devrait-on dire. Nous nous rendons compte de certaines représentations qui ne dépendent pas de nous ; d’autres dépendent de nous, ou du moins nous le croyons ; où est la frontière ? On devrait dire : il pense, comme on dit : il pleut. »
Lichtenberg
Si nous consacrons ce court chapitre introductif à la notion de frontière, qui n’est pas à proprement parler une figure, à peine un linéament, c’est que l’édification de frontières constitue un préliminaire obligé, un moment indispensable à la constitution de toute figure, comme le trait qui débute le dessin.
Ainsi que le remarque Cassirer,
« c’est une des tâches les plus importantes de la critique générale de la connaissance que de formuler les lois selon lesquelles on pose ces frontières dans le domaine théorique, avec les méthodes de la pensée scientifique. Elle montre que l’être « subjectif » et l’être « objectif » ne s’opposent pas dès le départ comme des sphères immuablement dissociées, parfaitement déterminées quant à leur contenu, et que l’un et l’autre n’acquièrent leur précision conceptuelle que dans le procès de la connaissance et en fonction des moyens et des conditions de celle-ci. »[7]
Nous voudrions, en nous inspirant de cette démarche, donner brièvement quelques exemples de l’intervention de frontières dans les domaines scientifiques, afin d’illustrer les principales acceptions de cette notion. Puis, les confrontant avec des conceptions plus générales de la frontière, nous serons conduits à nous interroger sur les conséquences psychologiques de cette pose ou dissolution de frontières, et plus précisément à distinguer, suivant la manière dont le cloisonnement s’effectue, deux grands types de figures intuitives.
Exemples de « frontières » dans les domaines scientifiques
C’est dans la notion d’ 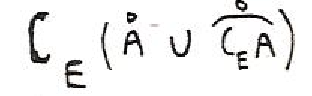 ensemble, en mathématiques, que nous devons semble-t-il rencontrer la notion de frontière dans sa plus grande généralité. En effet, la constitution d’un ensemble exige qu’on puisse dire de tout objet de pensée s’il est ou non compris dans l’ensemble, et qu’à « l’extérieur d’un certain cercle fermé de choses délimitables au moyen d’un principe donné, on n’ait plus d’élément de l’ensemble »[8].Si seuls sont définis logiquement l’ensemble et son complémentaire, puisqu’aucun élément ne peut échapper à cette dichotomie radicale, on voit que dans la formulation même de la pensée, dans la représentation intuitive ou graphique, il est nécessaire de recourir à l’image d’un contour délimitant : « à l’extérieur d’un certain cercle fermé », ou tout aussi bien « d’un côté d’une certaine droite ». C’est seulement en topologie, étude des localisations et des formes spatiales, que la frontière est reconnue comme entité à part égale, entre l’objet distingué et le domaine négligé ; cependant elle est conçue comme seconde vis à vis de cet intérieur et de cet extérieur prépondérants, puisqu’elle est définie comme la différence
ensemble, en mathématiques, que nous devons semble-t-il rencontrer la notion de frontière dans sa plus grande généralité. En effet, la constitution d’un ensemble exige qu’on puisse dire de tout objet de pensée s’il est ou non compris dans l’ensemble, et qu’à « l’extérieur d’un certain cercle fermé de choses délimitables au moyen d’un principe donné, on n’ait plus d’élément de l’ensemble »[8].Si seuls sont définis logiquement l’ensemble et son complémentaire, puisqu’aucun élément ne peut échapper à cette dichotomie radicale, on voit que dans la formulation même de la pensée, dans la représentation intuitive ou graphique, il est nécessaire de recourir à l’image d’un contour délimitant : « à l’extérieur d’un certain cercle fermé », ou tout aussi bien « d’un côté d’une certaine droite ». C’est seulement en topologie, étude des localisations et des formes spatiales, que la frontière est reconnue comme entité à part égale, entre l’objet distingué et le domaine négligé ; cependant elle est conçue comme seconde vis à vis de cet intérieur et de cet extérieur prépondérants, puisqu’elle est définie comme la différence 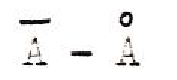 (adhérence de l’ensemble A moins son intérieur) ou encore comme ( complémentaire dans l’ensemble E de l’intérieur et de l’extérieur). Cette notion ne correspond bien à l’intuition que pour les espaces connexes (d’un seul tenant).
(adhérence de l’ensemble A moins son intérieur) ou encore comme ( complémentaire dans l’ensemble E de l’intérieur et de l’extérieur). Cette notion ne correspond bien à l’intuition que pour les espaces connexes (d’un seul tenant).
 Ailleurs peuvent exister des parties à la fois ouvertes et fermées , et qui donc n’ont pas de frontière. La topologie nous a par ailleurs habitués à bien des formes paradoxales, qui n’ont ni « intérieur » ni « extérieur » telle la « bouteille de Klein ». De même, Brouwer a pu construire une courbe frontière entre trois pays, telle que chacun de ses points soit un point triple[9], où là encore l’intuition immédiate est en défaut :
Ailleurs peuvent exister des parties à la fois ouvertes et fermées , et qui donc n’ont pas de frontière. La topologie nous a par ailleurs habitués à bien des formes paradoxales, qui n’ont ni « intérieur » ni « extérieur » telle la « bouteille de Klein ». De même, Brouwer a pu construire une courbe frontière entre trois pays, telle que chacun de ses points soit un point triple[9], où là encore l’intuition immédiate est en défaut :
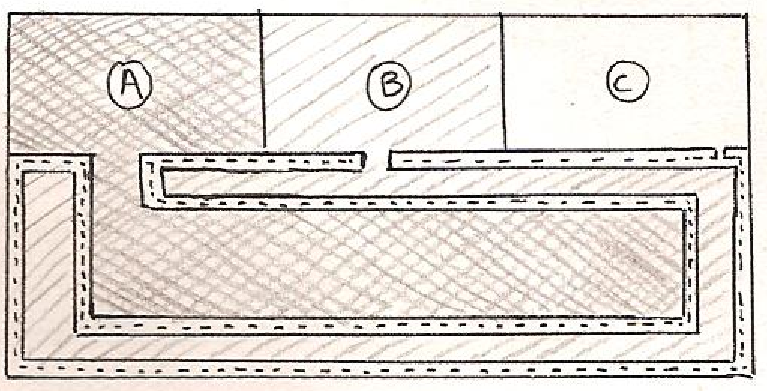
Chaque pays A, B ou C émet un prolongement qui reste à une distance x/n des autres. Pour obtenir la courbe des points triples, on fait tendre n vers l’infini.
Mais c’est principalement en analyse que la frontière vient à jouer un rôle authentiquement positif : la résolution d’une équation différentielle pose en effet un problème de conditions initiales, ou aux limites[10]; le « problème de Dirichlet » est à ce titre particulièrement instructif : il s’agit de démontrer l’existence d’une fonction f de trois variables x,y,z continue de classe C2 et telle que le laplacien de f
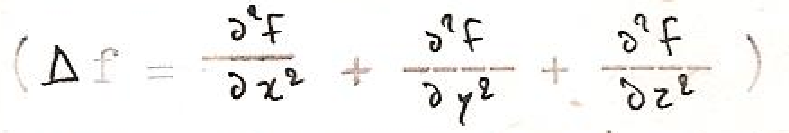
soit nul à l’intérieur d’un volume V (la fonction est alors dite harmonique) et telle que f prenne des valeurs données à l’avance sur la frontière S de V. Ce problème régit un grand nombre de cas physiques : on impose par exemple une température donnée sur une enceinte, et on demande la température intérieure, à l’équilibre. Il est clair que la connaissance de la température en tout point intérieur de V ne dépend que de sa position, et des valeurs fixées à la frontière.
A ces fonctions harmoniques est liée la théorie des fonctions holomorphes (si z = x + iy est un nombre complexe de C, une fonction f de C est holomorphe, grossièrement, si elle ne dépend que de z ; c’est donc une fonction à deux variables exprimable en fonction d’une seule variable complexe). Toute fonction harmonique peut être considérée comme la partie réelle d’une fonction holomorphe : on ne s’étonnera donc pas de retrouver chez ces dernières une relation étroite entre frontière et intérieur, qu’exprime la formule de Cauchy :
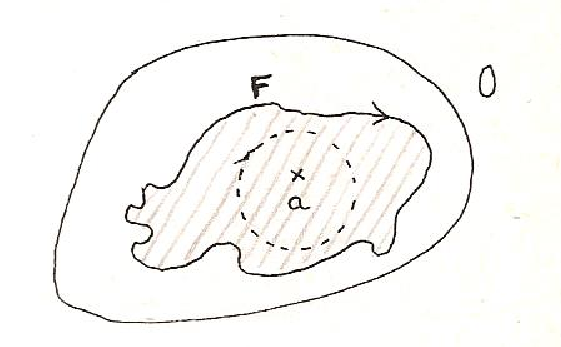 si f est holomorphe sur l’ouvert 0 de C, si F est une ligne frontière entourant le point a de 0 (homotope à un cercle), alors la valeur de f au point a est entièrement déterminée par le parcours des valeurs de f sur la frontière ; plus précisément, on a :
si f est holomorphe sur l’ouvert 0 de C, si F est une ligne frontière entourant le point a de 0 (homotope à un cercle), alors la valeur de f au point a est entièrement déterminée par le parcours des valeurs de f sur la frontière ; plus précisément, on a :
De par la simplicité de leur détermination, les fonctions harmoniques constituèrent pour les physiciens du XIX siècle une sorte d’idéal. Des techniques furent trouvées en analyse vectorielle, permettant également de ramener une étude sur un domaine à une étude sur sa frontière, basées sur les formules
- de Stockes :
 de Green-Ostrogradski :
de Green-Ostrogradski :
le flux du rotationnel d’un vecteur E à travers une surface fermée S est égal à la circulation de E sur la frontière C de la surface
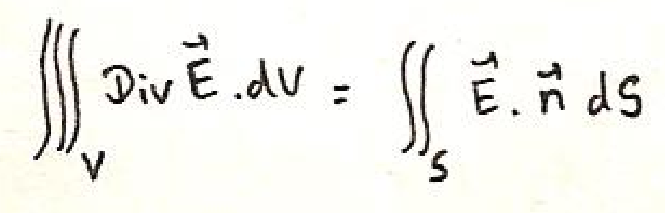
L’intégrale de la divergence de E sur un volume V est égale au flux de E à travers la frontière S

Le choix des conditions aux limites ou initiales est donc fondamental pour la résolution de toute équation différentielle. Si dans certains cas, comme nous l’avons vu, la donnée des conditions aux limites suffit à déterminer globalement la fonction dans tout son domaine d’existence, il est d’autres cas où on peut la déterminer seulement au voisinage de ses conditions initiales[11].
 Pour illustrer cette importance des conditions aux limites, citons en cosmologie l’équation poissonnienne qui lie le potentiel de gravitation à la densité locale de matière. Ce type d’équation nécessite une solution globale, et donc suppose de définir des conditions aux limites. Pour tourner la difficulté lorsqu’on l’applique à l’univers entier, Einstein, dans son premier modèle cosmologique d’univers « cylindrique », a supposé a priori que l’espace est une figure fermée, analogue à une sphère de dimension 3 dans un espace euclidien fictif de dimension 4 (il ne s’agit nullement du continuum espace-temps à 4 dimensions, qui lui est réel)[12]. Comme la sphère habituelle de dimension 2 dans l’espace de dimension 3, cette sphère fictive est à la fois figure de clôture, délimitant un monde intérieur fermé, et figure, sur sa frontière, d’un monde où un déplacement indéfini est possible.
Pour illustrer cette importance des conditions aux limites, citons en cosmologie l’équation poissonnienne qui lie le potentiel de gravitation à la densité locale de matière. Ce type d’équation nécessite une solution globale, et donc suppose de définir des conditions aux limites. Pour tourner la difficulté lorsqu’on l’applique à l’univers entier, Einstein, dans son premier modèle cosmologique d’univers « cylindrique », a supposé a priori que l’espace est une figure fermée, analogue à une sphère de dimension 3 dans un espace euclidien fictif de dimension 4 (il ne s’agit nullement du continuum espace-temps à 4 dimensions, qui lui est réel)[12]. Comme la sphère habituelle de dimension 2 dans l’espace de dimension 3, cette sphère fictive est à la fois figure de clôture, délimitant un monde intérieur fermé, et figure, sur sa frontière, d’un monde où un déplacement indéfini est possible.
Nous n’en dirons pas plus sur ces différentes interventions de la notion de frontière dans les domaines scientifiques. Si elle se révèle absolument indispensable à la pensée opératoire, puisque la solution d’un problème dépend avant tout du domaine sur lequel on l’envisage, elle n’en reste pas moins souvent, lorsqu’on ne peut en faire abstraction, une source de difficultés multiples, une irritante discontinuité : le bord d’une figure n’est-il pas, au sens de R. Thom, un « fermé des catastrophes » ?
Exemples de « frontières » hors des domaines scientifiques
Hors du domaine spécifiquement scientifique, la notion de frontière, de limite, de bord, voit s’accentuer cette double nature figure à la fois créatrice : « sans limite il n’y a pas de forme, sans forme il n’y a pas de perfection [13]», protectrice, matricielle, elle est en même temps borne, restriction à la liberté investigatrice de l’esprit.
Pour Parménide, dont la cosmologie est avant tout une méditation sur la sphère, 1’Etant
« est cette masse pareille à une sphère harmonieusement ronde, qui partout s’écarte également de son centre ; il n’est pas non plus de non-étant qui l’empêche de s’étendre en proportions égales…du centre jusqu’à son extrême achèvement rayonne son être homogène, souverainement…[14] »
Il n’est donc pas ici question de frontière, puisqu’elle séparerait l’Etant du Non-Etant, c’est à dire de rien. L’Etant n’est cependant pas libre d’une expansion illimitée, il est nécessaire d’informer cette masse rayonnante :
« la puissante nécessité le maintient étroitement dans des limites qui l’enserrent de toute part. Par conséquent, il n’est pas possible que l’Etre soit infini. En effet il ne lui manque rien, et s’il était infini il manquerait de tout. [15]«
Dans ces deux fragments apparaît tout l’embarras – qui culmine dans le paradoxe final – de l’esprit confronté à cette notion de frontière, à la fois atteinte à la perfection idéale, et condition de cette perfection ; seule la figure de la sphère permet de concilier logiquement (la puissante Nécessité) ces deux exigences d’une liberté (expansion harmonieuse, en proportions égales) et d’une forme (qui se crée en quelque sorte de manière purement interne, sans qu’il soit nécessaire de la contraindre par une quelconque barrière).
Figure d’enfermement, mais aussi de protection, telle apparaît la frontière dans la cosmologie d’Empédocle, sphérique elle-aussi [16]:
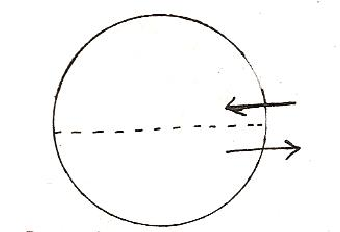
Lors de l’Age d’Or, le monde de la Lutte est au-dehors, le monde de l’Amour au dedans. Mais la barrière n’est pas étanche, et progressivement la Lutte s’infiltre et s’échappe 1’Amour, jusqu’à ce que plus tard le mouvement s’inverse, en un cycle éternel.
Nous n’irons pas plus loin dans ce dialogue du dedans et du dehors, de l’intérieur et de l’extérieur, aux si profondes résonances affectives, et dont Bachelard a montré le rôle essentiel, notamment dans les conceptions alchimiques[17].
Comme dernier exemple du compromis entre une pensée nécessairement cloisonnante et une intuition unificatrice, qui s’exprime dans la notion de frontière, nous voudrions nous attarder quelque peu sur une démonstration de Spinoza (12)[18] : tandis que chez Parménide une Nécessité contenait assez mystérieusement l’Etant à l’intérieur d’une limite, aucune raison logique ne s’oppose, chez Spinoza, à la libre expansion de la substance divine. Dans le Livre I de l’Ethique, supposant au départ une multiplicité de substances conçues comme des entités cloisonnées, absolument disjointes, il montre comment l’une d’entre elles, Dieu, se développe irrésistiblement jusqu’à annuler les autres. Dans la démonstration qui nous occupe, l’existence de Dieu est prouvée par l’inexistence d’une raison qui l’empêcherait d’exister (on pourrait dire tout aussi bien de s’étendre). Cette démonstration constitue comme le négatif de l’argument ontologique (voir Annexe III : La méthode de la diagonale et la construction de cercles vicieux) selon lequel l’existence est interne à l’idée de Dieu :

Il est clair que toute la démonstration avec cette curieuse conception d’une raison comme localisée, est sous-tendus par des images spatiales où la notion de frontière – quoique devant être finalement répudiée – joue un rôle prépondérant.
La puissance et l’universalité de cette problématique de l’intérieur et de l’extérieur font soupçonner d’importantes bases psychologiques, qui ont été étudiées notamment par les psychologues Rubin et Britsch : pour ce dernier, la condition primordiale de la pensée visuelle est que « quelque chose de voulu se détache d’un milieu non voulu (apeiron) au moyen d’un contour délimité »[19].
Peut-être faut-il chercher la genèse de cette notion de frontière dans la construction progressive de la personnalité « à partir d’un « absolu indifférencié de moi et d’environnement », d’une « conscience protoplasmique » – selon le mot de Piaget – de symbiose avec l’univers. Pour Freud :
« A l’origine,l’ego inclut tout, plus tard il détache de lui-même le monde extérieur. Le sens du moi que nous avons à présent n’est donc que le vestige retréci d’un sens beaucoup plus large – sens qui embrassait l’univers et exprimait une connexion inséparable de l’ego avec le monde extérieur. Si l’on peut supposer que ce sens primitif de l’ego a été préservé dans une mesure plus ou moins grande dans l’esprit d’un grand nombre d’hommes, il coexisterait comme une sorte de contrepartie avec le sens de l’ego de la maturité,plus étroit et plus nettement dessin, et son contenu idéationnel serait précisément la notion d’étendue sans borne et d’unité avec l’Univers.[20]«
Ce « sentiment océanique » est-il la contre-partie du cloisonnement inhérent à la pensée opératoire ? Il flotte en tout cas, associée à l’idée de frontière, comme la nostalgie d’une intimité perdue, qui s’exprime magnifiquement dans ce passage de Cassirer, à propos de l’intuition bergsonnienne :
« La pensée n’a son objet qu’en le « projetant » devant elle à une certaine distance où elle le considère. Toute union avec l’objet, si proche soit-elle, y signifie donc de ce fait une séparation de lui; toute conjonction devient une extériorité. Si on veut en venir à une unité véritable, au sein de laquelle être et savoir, au lieu de rester simplement face à face, s’interpénètrent vraiment, il faut qu’il y ait une forme première du savoir qui ait surmonté ce procédé de la spatialisation, de la mise à distance. Peut seule s’appeler métaphysique…la connaissance qui, libérée des contraintes du symbolisme spatial, se tient et se maintient au centre de l’étant par une pure vision intérieure, au lieu de chercher à capter cet étant au moyen de métaphores et d’images empruntées à l’espace.[21]«
Est-il vraiment possible de s’abstraire de ce symbolisme spatial ? Les figures de l’intuition que nous allons maintenant décrire semblent prouver le contraire. Il nous a semblé possible de les séparer en deux grandes classes, suivant justement leur rapport à la notion de frontière : de nombreux auteurs considèrent que le passage à l’époque moderne a été marqué par la rupture épistémologique entre la conception médiévale d’un espace centré, borné, et l’infinité homogène de l’espace cartésien. Ainsi, G. Canguilhem fait remarquer que
« dans le succès du terme « milieu » (en biologie), la représentation de la droite ou du plan indéfiniment extensibles, l’un et l’autre continus et homogènes, sans figure définie et sans position privilégiée, l’emporte sur la représentation de la sphère ou du cercle, formes qui sont encore qualitativement définies et, si l’on ose dire, accrochées à un centre de référence fixe.[22]«
Nous avons essayé de reprendre cette distinction, suivant le présupposé qu’une frontière « fermée » (cercle, sphère), séparant le champ réflexif en deux parties inégales, l’une infinie et l’autre finie, et apte à toutes les contractions et dilatations, ramène à l’idée de l’Un, ou du Tout indifférencié ; et qu’au contraire une frontière « ouverte » (ligne droite, plan) induit une coupure irrémédiable entre deux parties égales, adverses ou contraires, ce qui en fait la figure privilégiée de toute dualité.
La frontière devient alors dans le premier cas la contrainte à l’expansion de l’objet voulu, qu’il s’agit de lever ; dans le second cas, la barrière nécessaire entre deux expansionnismes équivalents.
![]()
FIGURES DE L’UN : LE CERCLE, LA SPHERE
D’une manière très générale, tout contour fermé, si complexe soit-il, concentrant l’attention sur un domaine clos au détriment d’un extérieur que l’on néglige, peut être considéré comme une représentation de l’Un[23]. Cependant la sphère ou le cercle (d’un point de vue intuitif, il n’y a pas lieu de distinguer les deux cas) reviennent à ce titre, du moins dans la tradition occidentale, avec une fréquence particulière. Nous nous limiterons donc à cette figure sphérique ou circulaire, le point (point fixe, centre…) en constituant un cas limite.
Les raisons d’une telle. hégémonie sont diverses : symétrie parfaite, simplicité maximale, commodité de représentation, analogies nombreuses avec des phénomènes naturels : nous en donnerons un inventaire rapide.
Quelques exemples de métaphores classiques, parfois de véritables modélisations basées sur la sphère illustreront ensuite l’importance de cette figure pour la pensée intuitive.
Nous consacrerons un paragraphe à des cas où interviennent la dilatation ou la contraction de la sphère, comme figuration du passage du local au global, du discret au continu.
Enfin,dans un dernier développement, nous verrons que cette figure (par emboîtements successifs, juxtaposition et imbrication), ou plus spécialement sa forme « duale », l’étoile, se prêtent particulièrement bien à l’expression de la multiplicité : il semble que l’Un et le Multiple soient deux notions très voisines du point de vue de la représentation intuitive, sans doute du fait de leur commun caractère d’indifférenciation : homogénéité interne à l’Un ou indiscernabilité entre éléments du Multiple.
Pourquoi la sphère ?
L’Univers est sphérique :
« soit parce que cette figure est la plus parfaite, soit parce qu’elle donne la plus grande capacité et par conséquent convient le mieux pour ce qui doit contenir toute chose ; soit encore parce que toutes les parties de l’Univers qui sont parfaites, le soleil, la lune et les étoiles sont ainsi formées ; soit encore parce que toutes les choses ont tendance à prendre cette forme, comme on le voit par les gouttes d’eau et des corps liquides en général [24]« .
Telles sont, exposées par Copernic,les principales raisons – d’ordre à la fois logique et analogique – du choix si fréquent de la sphère comme figure de 1’Un, c’est-à-dire d’une totalité indifférenciée.
Reprenons brièvement cette liste, et complétons-la :
- figure parfaite, elle est l’image de
- la simplicité (symétrique par rapport au centre et à tout plan passant par le centre) ;
- la permanence, au même titre que la spirale logarithmique, avec qui elle partage la propriété remarquable de se transformer en elle-même par un groupe continu de rotations (cette propriété merveilleuse inspira l’épitaphe de Bernouilli, le découvreur de la seconde figure : « eadem mutata resurgo ») ;
- l’équilibre, la stabilité, du fait de l’égale longueur de tous ses rayons : cette régularité, interdit toute transformation autre que l’expansion ou la rétraction isotrope autour du centre, lequel est généralement perçu comme immobile.
- figure maximale : elle représente à la fois la plus grande indétermination (puisque possédant toutes les symétries) et se détermine justement comme un maximum (plus grand rapport volume/surface, par exemple).[25]
- figure de clôture :
« Il donna à l’ensemble un arrondi externe, une surface parfaitement finie et lisse. Le monde n’avait pas besoin d’yeux, puisque rien de visible n’était laissé au dehors. Ni d’oreilles, puisqu’il n’y avait rien d’audible au dehors. » Platon, Timée[26].
- figure du cycle : conciliation des extrêmes temporels :
« Dans la circonférence d’un cercle, le commencement et la fin se confondent ». Héraclite.
« Toujours et partout, le vrai symbole de la nature est le cercle, parce qu’il est le schéma du retour périodique[27]« . Schopenhauer.
Métaphores et modèles sphériques
La coordination de telle ou telle de ces intuitions immédiates, ou la prise en compte d’une seule caractéristique privilégiée, ont donné naissance à une grande diversité de constructions intellectuelles qu’il serait vain de vouloir épuiser et classer ; en voici quelques exemples épars, qui vont de la simple métaphore au modèle véritable.
Le cercle,métaphore de l’éternité
« Un point donné de la circonférence, bien qu’indivisible,ne coexiste pas cependant avec tous les autres points, car l’ordre de succession constitue la circonférence ; mais le centre, qui est en dehors de la circonférence, se trouve en rapport immédiat avec quelque point donné que ce soit… L’ éternité ressemble au centre du cercle ; bien que simple et indivisible, elle comprend tout le cours du temps, et chaque partie de celui-ci lui est également présente[28]« . St Thomas d’Aquin.
Le cercle est ici utilisé classiquement pour représenter le temps (la sphère ne permettrait pas de figurer un ordre de succession), mais son caractère cyclique n’est pas développé. Le centre est conçu – nous en verrons d’autres exemples – comme point relié à tous les éléments d’une multiplicité.
La sphère, figure trinitaire
Pour Kepler,
« L’image du Dieu en trois personne réside dans la surface sphérique : ce qui signifie que le Père se trouve au centre, le Fils à la surface extérieure et le Saint Esprit dans l’égalité du rapport qui unit le point à la circonférence.[29]«
On sait, de l’aveu même de Kepler, qu’une analogie entre Dieu le Père et le soleil, le premier agissant par l’intermédiaire du Saint-Esprit, le second par l’intermédiaire d’une force physique, est à l’origine de ses conceptions astronomiques :
« j’ai cru d’abord, et très fermement, que la force motrice d’une planète était une âme. [30]« .
Cependant, ce recours à la sphère comme figure de la Trinité, presque un poncif du mysticisme, recèle des possibilités de variation notables :
| St Thomas d’Aquin | Nicolas de Cues, Kepler | Jacob Boehme | |
| centre | la créature insignifiante | Dieu | Fils |
| rayons | Saint Esprit | Saint Esprit[31] | |
| surface externe | Dieu | Fils | Dieu. |
Ces inversions et flottements montre que si les auteurs chrétiens choisissent la sphère comme métaphore trinitaire, c’est moins parce qu’elle se prête à une tripartition qui manque apparemment d’évidence intuitive, que pour reprendre une tradition mystique presque universelle de représentation du divin.
Ainsi Plotin, qui dissèque pourtant la sphère en ses éléments constitutifs d’une manière semblable, n’introduit aucune ternarité. L’utilisation plotinienne de la sphère, dont l’image hante les Ennéades, mérite que nous nous arrêtions ; car elle révèle toute une mécanique interne à la figure et qui semble mener la pensée plutôt que lui servir simplement d’illustration on peut donc parler proprement d’un modèle sphérique chez Plotin:
- la sphère elle-même représente l’Univers ;
- ses grands cercle, les êtres animés ;
- ses rayons, les intelligibles ;
- son centre représente en tant que :
- centre de grand cercle, une âme individuelle ;
- extrémité d’un rayon, une intelligence ;
- centre de toute la sphère,l’Un.
Il y a un centre au bout de chaque rayon, mais tous coïncident : en l’Un se confondent toutes les intelligences et les âmes individuelles. Mais surtout, de l’Un rayonnent toutes choses :
« le centre n’est point les rayons ni le cercle : il est leur père et il leur donne une trace de lui-même. Restant en son immobilité, il les engendre par une force qui est en lui et ils ne se séparent point de lui ».
Ainsi successivement le centre engendre les rayons, les rayons les grands cercles et les grands cercles la sphère tout entière. Il contient donc toute la sphère en puissance[32].
La sphère sénaire d’Abellio.
Dans son ouvrage La structure absolue, le philosophe et ésotériste R. Abellio propose un modèle universel d’explication basé sur la sphère.
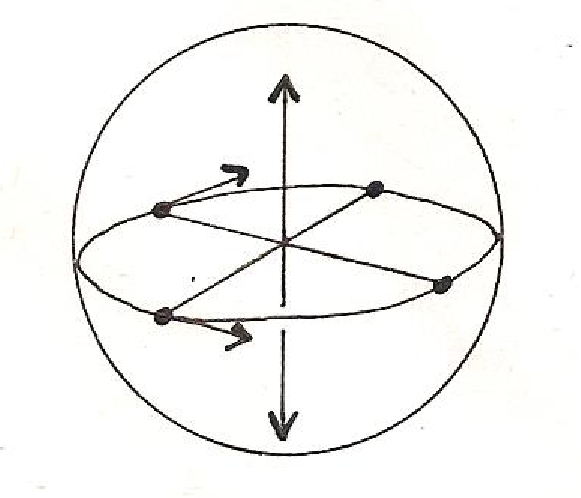 La quaternité –« quatre pôles répartis en deux couples antagonistes, qui engagent le mouvement dialectique par deux rotations en sens inverse » – est le fondement des phénomènes. La « structure absolue » prend ainsi l’image d’une sphère dont les quatre premières polarités, disposées en croix, occupent le cercle équatorial, tandis que les deux dernières figurent l’axe vertical de la rotation d’ensemble ». On obtient la figure de la sphère sénaire, qui permet la combinaison de deux rotations et de deux translations en sens inverse[33].
La quaternité –« quatre pôles répartis en deux couples antagonistes, qui engagent le mouvement dialectique par deux rotations en sens inverse » – est le fondement des phénomènes. La « structure absolue » prend ainsi l’image d’une sphère dont les quatre premières polarités, disposées en croix, occupent le cercle équatorial, tandis que les deux dernières figurent l’axe vertical de la rotation d’ensemble ». On obtient la figure de la sphère sénaire, qui permet la combinaison de deux rotations et de deux translations en sens inverse[33].
Le « module cosmique » de G.Lacroix
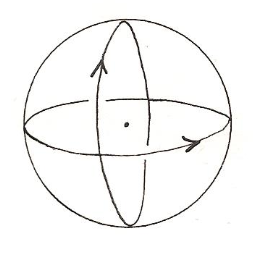
On a encore une structure quaternaire. Les modules cosmiques (4 types sont possibles) sont basés sur la rotation de deux sphères autour de deux axes orthogonaux[34].
:Une étude plus large des différentes et innombrables constructions basées sur la sphère, s’influençant les unes les autres ou constamment réinventées, permettrait de mieux cerner la part exacte de l’intuition. Mentionnons simplement qu’un aperçu historique est donné dans les « Métamorphoses du cercle », de G.Poulet, surtout d’un point de vue de critique littéraire. Selon cet auteur, l’âge médiéval serait celui des emboîtements hiérarchiques de sphères, l’âge baroque celui des interpénétrations et le XVIII° siècle celui de l’indépendance des sphères :« monde d’atomes non crochus condamnés à voltiger… sans jamais former un vrai monde ». De plus, le sujet de la métaphore aurait subi à cette époque un renversement, passant de Dieu à l’Homme : « L’homme au XVIIIe siècle n’embrassera plus du regard la sphère de Dieu, mais la sphère des connaissances scientifiques. L’encyclie divine deviendra une simple encyclopédie ».
Dilatation et contraction
Une homothétie centrée sur C, C étant le centre de la sphère, écarte ou rapproche de C tous ses points à la même vitesse, quelle que soit la direction. Cette propriété de « dilatation isotrope » constitue un dynamisme particulier à la sphère, et en fait une figure privilégiée du passage du local au global.
La tradition mystique est riche en métaphores utilisant ce dynamisme :
- pour Giordano Bruno, tout dans la nature est centré. La naissance d’un être est analogue. à l’expansion d’un cercle, la mort à sa contraction[35].
- Johannes Scheffler, mystique allemand du XVIIe siècle, écrit : « lorsque Dieu reposait, caché, dans les entrailles d’une vierge, le point contenait le cercle », et compare la dissolution de l’homme en Dieu à l’élargissement du centre vers la circonférence[36].
 Il est curieux de mettre en regard de ce texte le schéma mathématique, courant au début du XIX s siècle, qui visait à établir un paradoxe sur les infinitésimaux par le moyen de la dilatation et de la contraction simultanées de deux cercles 1 et 2.
Il est curieux de mettre en regard de ce texte le schéma mathématique, courant au début du XIX s siècle, qui visait à établir un paradoxe sur les infinitésimaux par le moyen de la dilatation et de la contraction simultanées de deux cercles 1 et 2.
On a en effet, par construction, égalité des surfaces hachurées. Lorsqu’on fait tendre PR vers AD, la « surface » du point P se trouve être égale à la « surface » de la ligne circulaire de rayon AD, ce qui semble absurde[37].
Dans les deux cas, le passage paradoxal entre deux quantités incommensurables, le point et la ligne, ou 1’homme et Dieu, est rendu possible par le recours à la métaphore sphérique.
Cette coïncidence n’a rien de très remarquable, car la dilatation ou la contraction du cercle, par sa simplicité, est couramment utilisée en mathématiques. Pour seul exemple nous citerons, en analyse, les lemmes de Jordan, qui permettent d’annuler l’intégrale sur un arc de cercle d’une fonction de la variable complexe, en faisant tendre le rayon de ce cercle vers l’infini : cette propriété est à la base du calcul d’intégrales par la méthode des résidus.
Plus généralement, on retrouve la notion de dilatation / contraction, en topologie, dans la notion d’homotopie : deux applications continues sont homotopes lorsqu’on peut passer de l’une à l’autre par une transformation continue. Ainsi, l’espace R, ou toute boule de cet espace, ont le « type d’homotopie » d’un point.
Citons enfin, en mathématique de la morphogenèse, la notion de « centre organisateur » dont R.Thom voit l’analogie, en physique, dans la théorie de l’explosion originelle, et en biologie dans le comportement exploratoire de l’embryon :
« je verrais volontiers l’Urbild de la spatialité, l’archétype fondamental de la notion d’espace, dans l’image d’un point-centre organisateur, qui s’étoile en une configuration sous-tendant tout un espace associé.[38]«
Nous reviendrons dans le paragraphe suivant sur cette notion d’élément rayonnant et de polycentrisme.
Concluons seulement que l’expansion du point en sphère, puis, par passage à la limite et abandon de la fixité du point, en « une sphère de rayon infini et dont le centre est nulle part[39] » est un moyen privilégié de passage d’un espace radial à un espace cartésien, d’un espace pointé à un espace homogène, et finalement peut-être, « d’un monde clos à un univers infini ».
L’Un et le Multiple
Emboîtements
L’expansion ou la rétraction de la sphère, non de manière uniforme, mais par pas discontinus, donne naissance à la figure des sphères concentriques emboîtées, dont on connaît l’importance pour toutes les cosmologies intuitives :
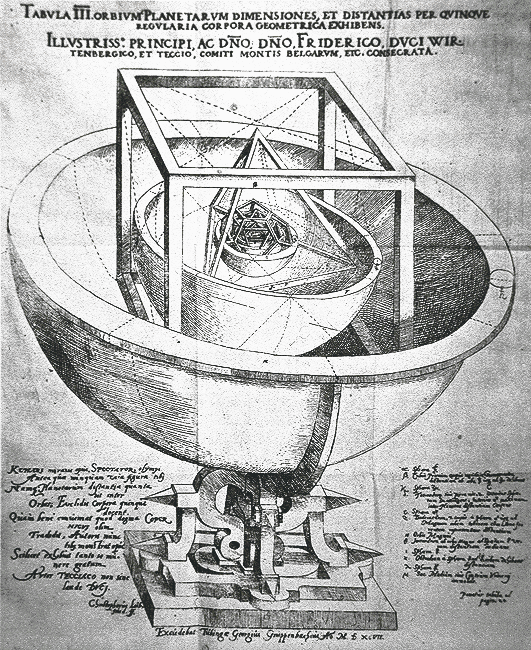
Modèle képlerien des orbites planétaires, entre lesquelles s’inscrivent les cinq solides parfaits
Une hiérarchie de mondes « gigognes » s’établit, entre lesquels jouent parfois des rapports subtils de proportionnalité : ainsi dans le « Phédon » de Platon, la Terre sphérique sur laquelle nous vivons est conçue comme un « creux » d’une Terre supérieure, notre ciel étant pour celle-ci une mer. Ceci explique le caractère corrompu des choses de ce monde, dont nous trouverions plus haut les correspondants plus purs, dans le même degré que l’air s’éloigne de l’eau et l’éther de l’air[40].
Ainsi donc, derrière la figure des sphères concentriques – cette itération indéfinie d’un Même – se profile souvent l’idée d’une ressemblance, d’une isomorphie entre étages : moins qu’une figure du Multiple, les sphères gigognes apparaissent encore comme une figure des modalités de l’Un[41].
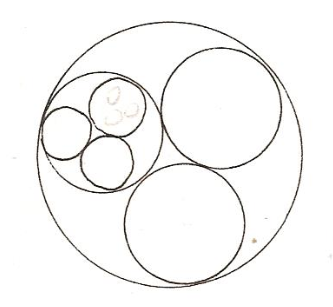 Cependant, l’emboîtement peut être plus complexe : ainsi Leibniz utilise la figure de l’emboîtement trois par trois de sphères non concentriques, comme modèle de sa théorie préformationniste de l’emboîtement des germes[42].
Cependant, l’emboîtement peut être plus complexe : ainsi Leibniz utilise la figure de l’emboîtement trois par trois de sphères non concentriques, comme modèle de sa théorie préformationniste de l’emboîtement des germes[42].
La projection sur un plan de cette construction donne une juxtaposition de cercles séquants, qui se « croisent sans se détruire » comme si l’on avait jeté dans de l’eau plusieurs pierres à la fois. M.Serres[43] y voit une figuration du polycentrisme leibnizien, fondement de la monadologie (voir notre Annexe I : La monade et ses avatars ): la monade est en effet définie comme un point de vue local, enfermée qu’elle est dans la sphère de ses perceptions, qui recoupe plus ou moins confusément celle des monades voisines. Cette figure des sphères juxtaposées et imbriquées préfigure assez exactement la notion moderne d’espace topologique, dans lequel tout est défini par des ‘relations de voisinage, c’est-à-dire des intersections de boules.
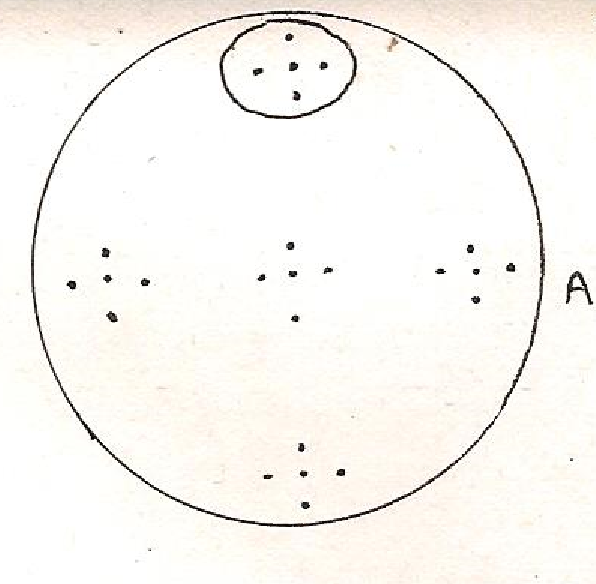 Un autre emboîtement du même type est le modèle d’univers pentadique de Fournier d’Albe (1907), proposé afin de résoudre la paradoxe d’Olbers (« ciel de feu »). On l’obtient à partir de cinq points disposés en croix, qu’on intrapole en remplaçant chaque point par le schéma entier, ou qu’on extrapole en considérant les 5 points comme un seul point du schéma. Quoique ne faisant pas appel à la figure plus élémentaire des sphères emboîtées, ce modèle mérite d’être cité car il répond à la même volonté intuitive d’hiérarchisation homogène[44].
Un autre emboîtement du même type est le modèle d’univers pentadique de Fournier d’Albe (1907), proposé afin de résoudre la paradoxe d’Olbers (« ciel de feu »). On l’obtient à partir de cinq points disposés en croix, qu’on intrapole en remplaçant chaque point par le schéma entier, ou qu’on extrapole en considérant les 5 points comme un seul point du schéma. Quoique ne faisant pas appel à la figure plus élémentaire des sphères emboîtées, ce modèle mérite d’être cité car il répond à la même volonté intuitive d’hiérarchisation homogène[44].
Une conception leibnizienne du monde, en réaction contre tout monocentrisme, semble avoir inspiré nombre d’auteurs contemporains, dans des domaines très divers : le zoologiste Von Uexküll insiste sur les caractéristiques perceptives propres à chaque animal (perception des couleurs, du temps…): « tout animal est entouré par son milieu spécifique rempli des caractéristiques auxquelles il est sensible, comme par une bulle de savon[45]« ; par analogie avec les comportements animaux, le sociologue E. T. Hall développe pour l’homme la même conception d’une bulle invisible, qui représente « notre distance personnelle, notre espace intime et vital[46]« ; on connaît enfin, en psychologie, les images de l’autisme ou de la schizophrénie comme « enfermement dans une coquille »…
Mais la limitation de cette figure des sphères juxtaposées tient à ce qu’elle suggère une collusion d’individus isolés, de noyaux durs se choquant les uns aux autres comme dans un chaos moléculaire, plutôt qu’une communauté d’unités compénétrantes, dont nous visualisons mal les imbrications. Lorsque c’est l’aspect relationnel entre ces diverses unités qui doit être souligné, l’intuition aura plus volontiers recours à une nouvelle série d’images.
Etoile
C’est encore à Leibniz que nous nous référerons, en reprenant les résultats, à valeur générale, de l’étude de M. Serres.
Une figuration privilégiée de la monade est en effet celle du point rayonnant, intersection d’un faisceau de droites, point focal, étoile. C’est en quelque sorte la figure duale, orthogonale de la sphère, que nous avons vu apparaître déjà chez Plotin. M.Serres dégage de cette figure deux propriétés intuitives:
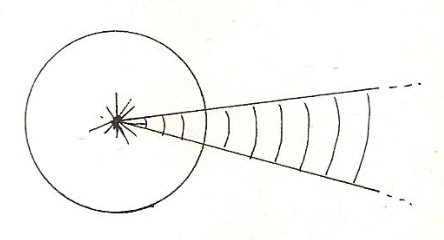 l’angle entre deux rayons restant fixe, elle est l’image d’une « information » qui se transmet sans changement de zéro à l’infini. Elle traduit « l’itération infinie (dans la similitude) d’une relation qui se propage d’un côté vers le monde, autant qu’on veut, de l’autre jusqu’à la limite centrale et ponctuelle » [47];
l’angle entre deux rayons restant fixe, elle est l’image d’une « information » qui se transmet sans changement de zéro à l’infini. Elle traduit « l’itération infinie (dans la similitude) d’une relation qui se propage d’un côté vers le monde, autant qu’on veut, de l’autre jusqu’à la limite centrale et ponctuelle » [47];
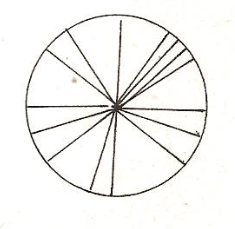
- d’autre part, elle permet de visualiser tous les angles possibles autour d’un point, donc « une multiplicité infinie d’itérations et de propositions analogues autour du point central, siège indivisible d’écartements en nombre infini »[48].
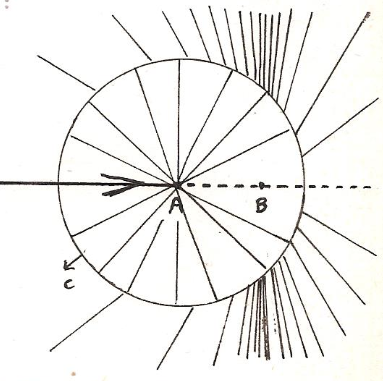 Nous voudrions mentionner un développement inattendu de ce schéma[49] pour expliquer qualitativement l’existenced’un rayonnement de freinage pour une particule chargée, .
Nous voudrions mentionner un développement inattendu de ce schéma[49] pour expliquer qualitativement l’existenced’un rayonnement de freinage pour une particule chargée, .
On peut représenter un électron par ses lignes de champ rayonnantes. Dans le cas d’un électron suffisamment rapide, l’effet relativiste peut être visualisé par un resserrement latéral des lignes de champ.
L’électron se déplace à une vitesse uniforme v. Au temps t0, on l’immobilise (freinage instantané) au point A. A l’instant t, il se trouverait en B si le mouvement uniforme avait continué. A l’intérieur d’une sphère de rayon ct, qui se dilate au cours du temps, on a le rayonnement isotrope d’une particule arrêtée. A l’extérieur, le rayonnement relativiste de l’électron avant l’arrêt. La discontinuité à la surface traduit l’existence d’un champ transversal intense, le rayonnement de freinage.
Réseau
Ces étoiles, facilement composables, se rassemblent dans la figure du réseau : M.Serres[50] oppose la conception cartésienne de la chaîne « qui concrétise pour l’imagination l’unicité de la progression et la liaison des raisons » à la conception leibnizienne du « réseau à plusieurs chaînes concourantes, qui préserve de multiples entrées et entrecroisements: tapisserie, tissage, broderie… » Il semble. que ces deux conceptions n’aient pas cessé de coexister à l’intérieur de la pensée scientifique, la première étant officiellement professée et la seconde constituant un idéal, une référence fascinante.
Ainsi R. Thom, dans son ouvrage sur l’imaginaire mathématique[51], brosse un remarquable tableau de la conception « magique » du monde, comme « ensemble finement réticulé » de sphères locales, le mythe précisant la « concaténation spatiale de ces sous-domaines, marqués chacun d’un centre à caractère sacré », la magie proprement dite traduisant la possibilité d’une action à distance entre ces différentes sphères. Le mathématicien C. Bruter[52], témoigne d’une image mentale personnelle qui semble se référer également à la figure du réseau :
« imaginez une Tour Eiffel, en modèle réduit, dont l’armature se compose de fils de verre qui laissent passer une lumière blanche, intense et diffuse, qui enveloppe la construction. Voilà la sensation, l’image curieuse que me laisse la géométrie ».
Dans un autre ouvrage[53], il définit la notion de « centre organisateur » en ces termes:
« le champ de force qui rayonne autour d’un germe de glace et transforme petit à petit des gouttelettes d’eau en cristaux est appelé champ morphogénétique. On dit qu’il rayonne ou se déploie à partir du centre organisateur. »
Ces exemples partiels font présager que la pensée mathématique (du moins certaines écoles) peut tirer son inspiration de figurations mentales très générales, qui hantent depuis toujours la pensée intuitive : monde magique de fils reliant tout à tout, toile d’araignée où tout se répercute à l’infini, où « tout est conspirant » selon l’expression de Pythagore, monde d’harmoniques et de correspondances. A l’image mentale révélée par C.P. Bruter semble répondre cette impression d’enfance de Lanza del Vasto, déterminante à ses yeux pour toute sa philosophie future[54]: après un matin de gel,
« devant moi, chaque pierre s’était changée en étoile, et des fils luisants la laient à la terre. Et je compris que le monde est un grand cristal qui se renvoie la lumière de facette en facette ».
La figure du réseau, comme forme désincarnée de la réalité, comme abstraction se déployant à un niveau supérieur, est particulièrement développée dans les deux réflexions suivantes, que sous-tendent clairement de puissantes représentations mentales :
- C.G.Hempel[55], dans une métaphore très poussée, insiste sur la dualité des niveaux, et les modes de correspondance entre eux :
« une théorie scientifique peut être comparée à un réseau spatial complexe : ses termes sont représentés par les noeuds du réseau, tandis que les fils qui relient ces derniers correspondent en partie aux définitions, en partie aux hypothèses primitives ou dérivées que renferme la théorie. Le système tout entier flotte pour ainsi dire au-dessus du plan d’observation, où il se trouve ancré au moyen de règles d’interprétation. On peut comparer ces règles à des chaînes qui n’appartiennent pas au réseau,mais en relient certaines parties à des régions déterminées du plan d’observation. Grâce à ces relations, qui servent à interpréter, le réseau peut remplir sa fonction de théorie scientifique : étant donné certains faits d’observation, nous pouvons remonter, par l’intermédiaire d’une chaîne d’interprétation, à un point précis du réseau théorique, et de là, par l’intermédiaire des définitions et des hypothèses, nous diriger vers d’autres points d’où une nouvelle chaîne d’interprétation nous permettra de regagner le plan d’observation ».
- chez Cassirer,la relation entre la notion d’abstraction et la figure du « réseau flottant » est presque systématique. Témoin ce passage[56] où l’entité abstraite, le signe, est perçu comme totalement détaché de ses points d’ancrage terrestres :
« La formule chimique abstraite…ne contient plus rien de ce que l’observation directe et la perception sensible nous font connaître de ce corps; mais au lieu de cela, elle place le corps particulier dans un réseau de relations extraordinairement riches et finement articulées, dont la perception en tant que telle ignore encore tout 1’ensemble des réactions, des rapports causals possibles, régis par des lois universelles… C’est la totalité de ces associations régulières que la formule de constitution chimique unit avec l’expression de la singularité… Le signe sert à créer une médiation qui permet de passer de la simple « matière » de la connaissance à sa « forme » spirituelle. C’est parce qu’il apparaît sans masse sensible propre, parce qu’il flotte en quelque sorte dans le pur éther de l’activité signifiante qu’il possède la faculté de mettre en scène, au lieu de simples détails de la conscience, le réseau complexe de ses mouvements. »
L’influence leibnizienne est sensible dans tout ce développement (multiple dans l’un, signe conçu comme élément d’un espace métaphysique, d’un « pur éther » ..) ; et c’est encore vers Leibniz que nous allons nous tourner pour découvrir un nouveau thème lié à l’intuition réticulaire : celui du point fixe.
Point fixe
Si les monades tissent bien un réseau entre elles, dans le plan de leurs perceptions réciproques, elles n’en restent pas moins selon une autre perspective radicalement incommunicantes. Leibniz utilise comme représentation de ce monde monadique un faisceau de droites parallèles, passant chacune par une monade, le parallélisme symbolisant à la fois la séparation (incommunicabilité) et l’identité de nature des monades. En un point à l’infini concourent toutes ces droites parallèles, c’est-à-dire coïncident les points de vue respectifs de toutes les monades. Ce point particulier est analogue au point géométral situé au sommet d’un cône, depuis lequel on ne voit plus la diversité apparente des corbes coniques, puisqu’on reconnaît leur nature commune d’intersection d’un plan avec le cône. Pour Leibniz, Dieu est ce point à l’infini depuis lequel le parallélisme des monades se change en perspective conique, et se restaure l’unité fondamentale du monde. Dieu est le « géométral de tous les points de vue » (30)[57]
Derrière la complexité analogique de cette construction s’exprime une intuition finalement assez simple : la figure du réseau, ensemble d’étoiles interreliées, fournit globalement l’image d’un monde homogène, parcourable en toute direction. Pourtant, vu en son lieu particulier, chaque noeud est un point distingué, qui entretient avec l’ensemble des relations uniques, individuelles. L’intuition d’un point fixe résulterait donc de la volonté de concilier en un seul lieu le point de vue local (on arrête le parcours indéfini du réseau par un point courant) et le point de vue global (le point géométral rassemblant néanmoins en lui, en image, les divers éléments de la multiplicité).
C’est l’artifice du « point à l’infini » qui permet la conciliation de ces intuitions géométriques contradictoires : c’est ce qui transparaît notamment chez Kant, dans la description d’une idée transcendantale. Elle a pour usage
« de diriger l’entendement vers un certain but, qui fait converger les lignes de direction suivies par toutes ses règles en un point qui, pour n’être il est vrai qu’une idée (focus imaginarius), autrement dit un point d’où les concepts de l’entendement ne partent pas réellement – puisqu’il se situe entièrement hors des bornes de l’expérience possible – sert néanmoins à leur procurer la plus grande unité avec la plus grande extension[58]« .
En résumé, il semble bien que le sentiment profond d’une liaison universelle des choses incline l’esprit à se représenter cette diversité de relations sous forme d’une entité abstraite, dépouillée de toute consistance sensible, d’un réseau qui flotte au dessus du plan des objets jusqu’à parfois s’en détacher complètement ; la figure du réseau conduit ensuite à particulariser un point fixe d’où une vision globale est possible. Un dernier exemple synthétise ces intuitions successives : pour Cassirer, il faudrait que la philosophie puisse « découvrir un point fixe qui
serait situé au-dessus de toutes ces formes (les différents aspects de la culture spirituelle), mais non pas cependant absolument au-delà d’elles: un point fixe d’où l’on pourrait les embrasser toutes d’un seul regard, et qui cependant ne donnerait à voir que les rapports purement immanents que toutes ces formes entretiennent en elles, et nullement leur rapport à quelqu’être ou quelque principe extérieur et transcendant[59]« .
Ainsi partant de l’Un figuré par la sphère, nous l’avons itéré au sein de multiplicités abstraites, pour revenir finalement à l’Un sous la forme d’un point à l’infini, d’un centre, d’un point géométral contenant toutes choses en lui. Il est clair que l’aspiration au point fixe que révèle cette progression particulière a un caractère bien plus général. M.Serres[60], au travers d’une longue analyse des travaux scientifiques de Pascal, démontre qu’ils sont tous parcourus par l’obsession du point fixe, la quête d’un centre pour l’homme, irrémédiablement au-delà de ses possibilités d’appréhension. Souvent le problème du point fixe recoupe celui, si longtemps débattu, du maximum d’une suite ordonnée :
- pour Platon, pour Saint Anselme, l’existence de choses justes ou bonnes impose l’existence de la Justice, ou du Bien souverains ;
- pour Bossuet, l’idée d’imparfait impose celle d’un Etre parfait ; car on ne conçoit pas qu’une comparaison entre les termes de la suite soit possible sans un point de référence fixe, situé à une extrémité, au-delà de notre perception, dans un infini actuel.
Sur les racines profondes de cette notion de point fixe – que l’on a peine à qualifier de figure tant elle est élémentaire, et en même temps certainement fondamentale pour de nombreux processus psychologiques, nous ne pouvons que renvoyer à une hypothèse de Cassirer[61] :1’étude clinique de l’aphasie (perturbations du sens spatial, de la capacité d’additionner des nombres…) démontre pour cet auteur la nécessité absolue de définir un point de départ, une origine stable, inhérente à certains de nos fonctionnements cérébraux.
–
![]()
FIGURES BINAIRES
« Les uns disent que c’est un caillou. Les autres disent que c’est un oiseau. En effet, c’est un oeuf. »
Lanza del Vasto, Principes et Préceptes du retour à l’évidence, p122.
« Dans l’oeuf il y a deux forces, celle qui tend à ce qu’il reste un oeuf et celle qui tend à ce qu’il devienne poussin. L’oeuf est donc en désaccord avec lui- même, et toutes choses sont en désaccord avec elles-mêmes. »
G.Politzer, Principes élémentaires de philosophie, p 185
Tandis que les figures de l’unité ou de la multiplicité, ainsi que nous l’avons vu, peuvent atteindre une certaine complexité géométrique, les figures de la binarité semblent beaucoup plus pauvres en représentations visuelles. Au contraire, du point de vue linguistique, la proportion est inversée, et une débauche de termes aux nuances très subtiles s’emploient à désigner les divers modes de la confrontation : les contradictoires, les contraires,les opposés, les inverses, les pôles, les complémentaires, les duaux, les extrêmes, les distincts, les différents… L’aspect « rhétorique » de la notion de figure prend nettement le pas sur son aspect « topologique ». Cependant, ici comme auparavant, nous aurons pour parti-pris de faire abstraction des racines linguistiques des concepts binaires, tout en restant conscient du caractère souvent arbitraire de cette discrimination.
Ainsi par exemple, selon le jugement de Cassirer, « le style de la langue d’ Héraclite et le style de sa pensée se déterminent réciproquement »: puisque dans le langage, tout sens est corrélatif à son contraire, de même la réalité, pour être exprimable, doit se trouver structurée en systèmes de couples antagonistes.
Nous ne tenterons donc pas de donner un sens précis aux divers termes énumérés plus haut, que des usages abusifs ont souvent malmenés et confondus. Témoin par exemple, ce raisonnement de Xénophane visant à prouver que Dieu est inengendré :
- ce qui naît doit naître soit du semblable, soit du dissemblable ;
- par raison de symétrie, le semblable ne peut pas naître du semblable. Car « il n’y a pas plus de raisons pour que l’un plutôt que l’autre engendre ou soit engendré ».
- d’autre part, si l’Etre naissait du dissemblable, il naîtrait par définition de ce qui n’est pas, ce qui est absurde.
Le caractère sophistique de l’argument provient évidemment de la confusion entre le contraire (Etre, Non-Etre) et le différent (dissemblable). Cependant cette erreur élémentaire est révélatrice d’une réelle difficulté conceptuelle : le « contraire » peut être en effet défini « le dissemblable en tout ». Sitôt que, dans un premier moment de la réflexion, l’esprit se limite à envisager une seule propriété binaire, la distinction entre différence et contrariété s’efface. C’est seulement par un processus d’induction portant sur la totalité des propriétés d’un objet que se constitue celle-ci à partir de celle-là.
Des difficultés de ce type rendent illusoire une formalisation de ces catégories, dès lors qu’elles fluctuent si largement au gré des convictions et des intentions de qui les utilise. Nous nous contenterons donc de définitions minimales, d’après l’intuition spatiale dont elles nous semblent relever :
- une séparation tranchée ( deux points distincts, plan coupant l’espace en deux parties) pourra dénoter les contraires ou les duaux (idée de symétrie) coexistant simultanément ;
- les complémentaires impliquent l’idée d’un balancement, d’un mouvement de va-et-vient entre les termes qui révèle la nécessité d’une saisie alternative ;
- les pôles, les extrêmes expriment une idée de continuité entre les termes (extrémités d’un segment par exemple)
Il semble parfois envisageable de distinguer la coupure gauche/droite, plutôt liée à la notion de symétrie[62], et la coupure haut/bas qui introduit une distinction de niveau. De même, en conformité avec une intuition physique évidente, la direction horizontale semble privilégier l’idée de continuité, de rapprochement ou d’extension sans rupture, tandis que la direction verticale impose un saut qualitatif, le « passage au plan supérieur », le « dépassement » d’une contradiction irrémédiable au niveau des termes initiaux[63]. (2)
Résultantes de perceptions physiques diffuses (la ligne d’horizon, la latéralité gauche-droite, la réflexion par un miroir, par un plan d’eau) et d’anisotropies inscrites au sein même de notre appareil sensoriel, ces figures ont un caractère complexe, mêlé, comparé à la clarté intuitive des figures unitaires. Car s’il est facile d’observer dans la nature des tendances au centrisme, au regroupement, à la forme sphérique, les phénomènes purement binaires y sont rares (miroirs, aimants, reproduction sexuée) et chargés de mystère. D’où des hésitations, des confusions, des superpositions fréquentes entre les figures qu’ils inspirent, plus ou moins indirectement.
C’est par contre le langage, ce monde où sans entrave se créent des paires de contraires, s’agglomèrent des racines en de nouvelles unités, qui fournit à la pensée binaire son principal matériau, son terrain d’expériences, sa source privilégiée d’analogies. A ce niveau d’abstraction supérieur, une construction intellectuelle se surajoute nécessairement aux intuitions immédiates : par là, la binarité ressortit avant tout d’une étude psychologique. On connaît les thèses de Wallon sur la préexistence des structures binaires, sur leur rôle essentiel dans la pensée relationnelle. De même Piaget a montré que, par exemple, le schème polaire action/résistance est un des premiers moments organisateurs de l’intelligence ; ou bien, étudiant comment de jeunes enfants reconstituaient la moitié cachée d’un objet, a mis en évidence la spontanéité de la notion de symétrie.
Nous ne pouvons développer l’exposé de ces recherches passionnantes. Qu’il nous suffise ici d’avoir mentionné ces deux déterminations fondamentales – linguistique et psychologique – de la pensée binaire et d’avoir marqué que celle-ci se situe, vraisemblablement, à un niveau différent de la pensée unitaire , plus abstrait, plus opératoire, moins instinctuel : si l’Un est le matériau du Mythe, le Deux est 1’instrument des Systèmes.
La binarité pure
.
Il est paradoxalement assez difficile de trouver des exemples de systèmes où se. confrontent uniquement des couples de principes, tant est forte la contamination du troisième terme et la tentation de l’échappée sur un autre plan. Le paradigme de la binarité pure pourrait être, bien sûr, la pensée d’Héraclite – si fragmentaire et difficile à saisir qu’elle nous soit parvenue – où l’énumération de couples de contraires, jointe à l’affirmation de leur identité profonde, prend presque rang de figure de style :
- « le chemin qui monte est le même que le chemin qui descend » (frag. 60)
- « Dieu est jour et nuit, hiver et été, guerre et paix, satiété et faim. Il se transforme comme le feu mêlé d’aromates: chacun le nomme à sa guise. » (fr. 67)
Ainsi l’harmonie repose sur la lutte, les transformations mutuelles et la confusion des contraires, dans le brasier qui est le principe universel. Cependant, nous retiendrons surtout de la pensée héraclitéenne cette magnifique image de l’harmonie par la tension interne:
- « Ils ne comprennent pas comment ce qui lutte avec soi-même peut s’accorder : mouvements en sens contraires comme pour l’arc et la lyre. » (fr. 51)
Peut-être pouvons nous retrouver, dans la définition de la polarité par Schopenhauer[64], cette même intuition d’un couple qu’une liaison élastique unit, vibrant sans cesse dans des alternatives de rapprochement et de séparation à la manière d’un dipôle électrique :
« …phénomène d’une activité se décomposant en deux moitiés qui se conditionnent mutuellement, qui se cherchent et tendent à se réunir à nouveau…Leur séparation se manifeste le plus souvent aussi dans l’espace par un mouvement dans deux directions opposées. »
 Profondément enracinée dans l’intuition d’un équilibre physique, comme le montre l’exemple d’Héraclite, cette idée d’une oscillation entre les contraires a reçu très tôt une interprétation d’ordre logique. Ainsi Platon, dans le Phédon, expose la théorie de leur génération réciproque : le « plus grand », par exemple, ne peut se concevoir que par accroissement à partir du « plus petit » ; on peut donc dire que le « grand » naît de son contraire, et réciproquement. Cette découverte de la continuité entre termes liés par une telle relation, et de la nécessité, afin que la nature ne soit pas « boiteuse », que tout parcours dans un sens soit compensé par un parcours en sens inverse, « comme si les choses qui existent accomplissaient un parcours circulaire », fournit immédiatement un argument contre l’irréversibilité de la Mort il faut que, par contrepoids, existe le passage inverse : revivre.
Profondément enracinée dans l’intuition d’un équilibre physique, comme le montre l’exemple d’Héraclite, cette idée d’une oscillation entre les contraires a reçu très tôt une interprétation d’ordre logique. Ainsi Platon, dans le Phédon, expose la théorie de leur génération réciproque : le « plus grand », par exemple, ne peut se concevoir que par accroissement à partir du « plus petit » ; on peut donc dire que le « grand » naît de son contraire, et réciproquement. Cette découverte de la continuité entre termes liés par une telle relation, et de la nécessité, afin que la nature ne soit pas « boiteuse », que tout parcours dans un sens soit compensé par un parcours en sens inverse, « comme si les choses qui existent accomplissaient un parcours circulaire », fournit immédiatement un argument contre l’irréversibilité de la Mort il faut que, par contrepoids, existe le passage inverse : revivre.
 Aristote, dans sa théorie de la matière, reprend cette idée de symétrie nécessaire: tout objet, avant d’être, pouvait être indifféremment ce qu’il est ou son contraire. C’est le mouvement, ou le désir, qui le faisant passer de la puissance à l’acte, le fige dans l’une ou l’autre forme, qui dès lors s’excluent.
Aristote, dans sa théorie de la matière, reprend cette idée de symétrie nécessaire: tout objet, avant d’être, pouvait être indifféremment ce qu’il est ou son contraire. C’est le mouvement, ou le désir, qui le faisant passer de la puissance à l’acte, le fige dans l’une ou l’autre forme, qui dès lors s’excluent.
Par ce mécanisme de saut entre deux niveaux, on évite la collusion des contraires dans une même entité : ils deviennent proprement des complémentaires, en ce sens que seule la réunion des deux termes permet d’expliquer l’Univers, mais que sitôt que l’un apparaît, l’autre s’efface, à la manière de ces dessins géométriques qui apparaissent tantôt en creux, tantôt en relief, suivant la manière dont on les regarde.
Nous devons à Stéphane Lupasco d’avoir réorganisé ces intuitions aristotéliciennes à la lumière des découvertes de la physique contemporaine. On sait comment la dualité onde-corpuscule, en mécanique quantique, a pu inspirer le besoin d’une nouvelle logique propre aux phénomènes microphysiques ; on connaît égaiement l’introduction par Bohr du principe de complémentarité, selon lequel ces deux descriptions, quoique étant nécessaires toute deux à une explication totale, s’excluent néanmoins l’une l’autre dans l’expérience.
 Nous ne mentionnons ce débat[65], qui semble d’ailleurs relativement passé de mode en physique, que parce qu’il est à la base de la problématique de Lupasco : ne pourrait-on en effet concevoir ce chassé-croisé des deux descriptions en termes de potentialisation/actualisation ? Actualisation de la particule potentialisant le champ sous forme d’onde de probabilité, actualisation du champ électro-magnétique potentialisant la particule sous forme de photon[66]. Plus généralement, toute réaction chimique, biologique, revient au passage d’un état potentiel à un état actuel, en potentialisant ce qui s’y opposait auparavant dans l’actualité. Ce balancement nécessite qu’à tout dynamisme corresponde un dynamisme en sens inverse : c’est le principe d’antagonisme.
Nous ne mentionnons ce débat[65], qui semble d’ailleurs relativement passé de mode en physique, que parce qu’il est à la base de la problématique de Lupasco : ne pourrait-on en effet concevoir ce chassé-croisé des deux descriptions en termes de potentialisation/actualisation ? Actualisation de la particule potentialisant le champ sous forme d’onde de probabilité, actualisation du champ électro-magnétique potentialisant la particule sous forme de photon[66]. Plus généralement, toute réaction chimique, biologique, revient au passage d’un état potentiel à un état actuel, en potentialisant ce qui s’y opposait auparavant dans l’actualité. Ce balancement nécessite qu’à tout dynamisme corresponde un dynamisme en sens inverse : c’est le principe d’antagonisme.
On voit donc comment se trouvent réunies dans cette conception l’exigence de compensation de Platon, et la distinction de niveaux d’Aristote. Cependant, rien n’empêche ici que dans leur passage simultané d’un état à l’autre, les deux contraires ne se rencontrent dans un même état intermédiaire entre l’actualisation et la potentialisation. Le principe aristotélicien du Tiers-Exclu n’est plus valable, ce qui compte est la considération dans un même tout des deux antagonismes symétriques. De même, Lupasco ne manque pas de prendre ses distances vis à vis de la dialectique hégélienne : ici,pas de troisième terme synthétique ; on peut simplement définir un « système » englobant plusieurs couples antagonistes, auquel s’opposera à son tour un système antagoniste, au sein d’un système de systèmes »[67]. Inutile également de chercher à échapper à la contradiction par passage au plan supérieur :
« La vie est carnage, l’âme est tourment. Et c’est dans la non-transcendances de cette contradiction, infiniment expansible, que s’engendre cette conscience de la conscience et cette connaissance de la connaissance qui se confondent avec sa nature même.[68]«
D’Héraclite à Lupasco se perpétue la même poésie tragique de l’opposition irrésoluble, de la contradiction source à la fois de Mort et de Vie. Cependant la recherche systématique de telles contradictions semble parfois manquer de pertinence : champ et particules, par exemple, représentent deux aspects distincts de la réalité, et il est difficile de les penser comme s’excluant l’un l’autre. Un exemple de système – ou plutôt de mise en forme assez humoristique – mettant en évidence le rôle créateur de la seule différence pourrait être le processus de « bissociation » qu’Arthur Koestler propose comme base de l’activité inventive :
« Lorsque deux matrices indépendantes de perception et de raisonnement interfèrent, le résultat sera :
- soit une collision aboutissant au rire (réaction HAHA),
- soit leur fusion en une nouvelle synthèse intellectuelle (réaction AHA),
- soit leur confrontation dans une expérience esthétique (réaction AH).[69] »
 Si donc, dans une certaine mesure, le processus inventif provient du rapprochement de deux termes auparavant disjoints (ainsi que le suggère le schéma ci-contre, emprunté à A.Koestler), l’efficacité d’un raisonnement dépend à l’inverse de la discrimination exacte des domaines sur lesquels il agit : c’est, à l’orée du raisonnement déductif, le principe de la méthode dichotomique. Mettant l’esprit, à chaque palier d’itération, face à deux possibilités qui s’excluent absolument, elle l’amène à définir, par emboîtements successifs,le statut exact d’un objet complexe. Ainsi que le montrent les exemples fameux du « Sophiste », c’est donc avant tout une méthode de classification et de clarification, qui permet de passer du général au particulier.
Si donc, dans une certaine mesure, le processus inventif provient du rapprochement de deux termes auparavant disjoints (ainsi que le suggère le schéma ci-contre, emprunté à A.Koestler), l’efficacité d’un raisonnement dépend à l’inverse de la discrimination exacte des domaines sur lesquels il agit : c’est, à l’orée du raisonnement déductif, le principe de la méthode dichotomique. Mettant l’esprit, à chaque palier d’itération, face à deux possibilités qui s’excluent absolument, elle l’amène à définir, par emboîtements successifs,le statut exact d’un objet complexe. Ainsi que le montrent les exemples fameux du « Sophiste », c’est donc avant tout une méthode de classification et de clarification, qui permet de passer du général au particulier.
 Remarquons qu’elle n’ajoute rien à l’objet initial: elle se contente de déployer au dessous de lui 1’arborescence de ses parties; Lue dans le sens ascendant, elle constitue une hiérarchie. Par là, elle est également une méthode relationnelle, en ce sens que, saisissant l’un dans le filet des sous-classes de l’autre, elle permet de montrer la dépendance de deux objets, et de donner une image de leur degré d’éloignement. Pour rappeler d’ailleurs cette inclusion constante dans le terme initial, Michel Serres[70] (9) propose de représenter la dichotomie sous forme d’une spirale se refermant sur elle-même, et convergeant vers l’objet recherché :
Remarquons qu’elle n’ajoute rien à l’objet initial: elle se contente de déployer au dessous de lui 1’arborescence de ses parties; Lue dans le sens ascendant, elle constitue une hiérarchie. Par là, elle est également une méthode relationnelle, en ce sens que, saisissant l’un dans le filet des sous-classes de l’autre, elle permet de montrer la dépendance de deux objets, et de donner une image de leur degré d’éloignement. Pour rappeler d’ailleurs cette inclusion constante dans le terme initial, Michel Serres[70] (9) propose de représenter la dichotomie sous forme d’une spirale se refermant sur elle-même, et convergeant vers l’objet recherché :
 Cependant, il n’y a dans ces propriétés taxinomiques rien qui soit lié absolument à la binarité : on peut parfaitement concevoir plus de deux termes à chaque niveau, à condition qu’ils soient disjoints. Un exemple de l’emploi du procédé dichotomique en mathématiques nous aidera à saisir le caractère moteur de cette binarité :
Cependant, il n’y a dans ces propriétés taxinomiques rien qui soit lié absolument à la binarité : on peut parfaitement concevoir plus de deux termes à chaque niveau, à condition qu’ils soient disjoints. Un exemple de l’emploi du procédé dichotomique en mathématiques nous aidera à saisir le caractère moteur de cette binarité :
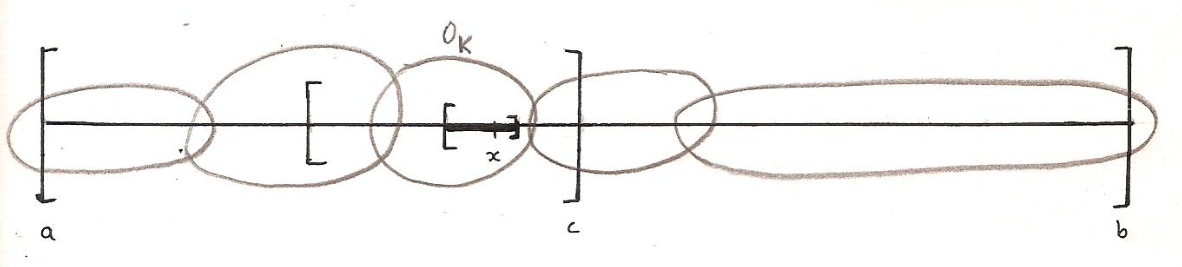 Nous nous proposons de démontrer que tout segment S0 = [a,b] de l’axe des nombres réels est compact. Supposons S0 non compact, ce qui signifie par définition qu’il existe un recouvrement O = Ui Oi de S0 par une infinité d’ouverts, dont on ne peut extraire aucun sous-recouvrement fini ( O est par exemple la réunion d’une infinité de boules recouvrant entièrement le segment S0). Divisons S0 en deux parties [a, c] et [c, b]. L’une au moins de ces deux parties n’est pas recouvrable de manière finie dans O (sinon leur réunion [a,b] serait recouvrable de manière finie dans O, contrairement à l’hypothèse) . Notons S1 cette partie. En réitérant cette opération, on obtient une série de segments emboîtés S0, S1, S2… Une propriété de ces segments dans l’ensemble des réels est qu’il existe un nombre x appartenant à leur intersection. Puisque x appartient à S0, il appartient également à une boule Ok du recouvrement O. On voit donc, puisque tous ces segments sont en quelque sorte centrés par x, qu’il existera un segment S, suffisamment petit pour être recouvert par la seule boule Ok. Or d’après leur choix, tous ces segments sont non-recouvrables de manière finie dans O. On aboutit donc à une contradiction, qui prouve la fausseté de l’hypothèse initiale.
Nous nous proposons de démontrer que tout segment S0 = [a,b] de l’axe des nombres réels est compact. Supposons S0 non compact, ce qui signifie par définition qu’il existe un recouvrement O = Ui Oi de S0 par une infinité d’ouverts, dont on ne peut extraire aucun sous-recouvrement fini ( O est par exemple la réunion d’une infinité de boules recouvrant entièrement le segment S0). Divisons S0 en deux parties [a, c] et [c, b]. L’une au moins de ces deux parties n’est pas recouvrable de manière finie dans O (sinon leur réunion [a,b] serait recouvrable de manière finie dans O, contrairement à l’hypothèse) . Notons S1 cette partie. En réitérant cette opération, on obtient une série de segments emboîtés S0, S1, S2… Une propriété de ces segments dans l’ensemble des réels est qu’il existe un nombre x appartenant à leur intersection. Puisque x appartient à S0, il appartient également à une boule Ok du recouvrement O. On voit donc, puisque tous ces segments sont en quelque sorte centrés par x, qu’il existera un segment S, suffisamment petit pour être recouvert par la seule boule Ok. Or d’après leur choix, tous ces segments sont non-recouvrables de manière finie dans O. On aboutit donc à une contradiction, qui prouve la fausseté de l’hypothèse initiale.
La démonstration repose clairement sur deux propriétés de la dichotomie compatibles avec celles intrinsèques des objets manipulés : le rétrécissement du domaine difficile, qui permet de le « centrer » puis de l’enclore, d’après des propriétés connues par ailleurs ; et une condition d’additivité, se propageant de proche en proche (si les parties étaient recouvrables de façon finie, la somme le serait également).
Cependant en dernière analyse, c’est la disjonction des classes qui est essentielle : l’étanchéité de la frontière garantit que, postérieurement à une étape donnée, les parties laissées de côté n’influeront pas sur la partie circonscrite.La binarité pure ne tient donc pas tant ici à la division par deux (la plus simple et la plus naturelle[71]) qu’à la distinction, à chaque étape, entre la partie négligée et la partie choisie. La dichotomie apparaît donc proprement comme une méthode raisonnée de concentration de l’esprit.
Le moyen terme
Si la dichotomie s’avère un instrument simple pour convaincre, pour ordonner, pour démontrer parfois, elle ne saurait rien nous apprendre sur le monde, puisqu’elle est la simple émanation de l’activité cloisonnante de l’esprit : Aristote, déjà, lui reproche cette stérilité. De plus, ce découpage en parties indépendantes, dont la somme est toujours égale au tout, apparaît bien sommaire: ainsi que le remarque Jean Rostand, « lorsqu’il s’agit de se représenter un phénomène naturel, la première démarche de l’esprit est souvent de pratiquer sur le réel d’illusoires dichotomie ». Ce caractère primitif de la division en classes disjointes est corroboré par la psychologie génétique : les jeunes enfants ne réussissent pas à rassembler des classes ayant un domaine commun, pour lesquelles la propriété d’additivité n’est pas conservée. L’introduction du « ou inclusif » en logique permet de lever la difficulté, mais introduit une propriété d’idempotence ( A ou A = A) moins familière à l’esprit[72] ; de même, Piaget a montré que l’acquisition de la transitivité, c’est à dire la constatation d’un dynamisme entre deux relations binaires juxtaposées, nécessitait un âge minimal.
Il semble bien que l’invention du syllogisme en logique corresponde à une extension de la méthode dichotomique suivant ces deux axes psychologiques :
- « horizontal » : passage des classes disjointes aux classes imbriquées ;
- « vertical » : considération de trois étapes successives.
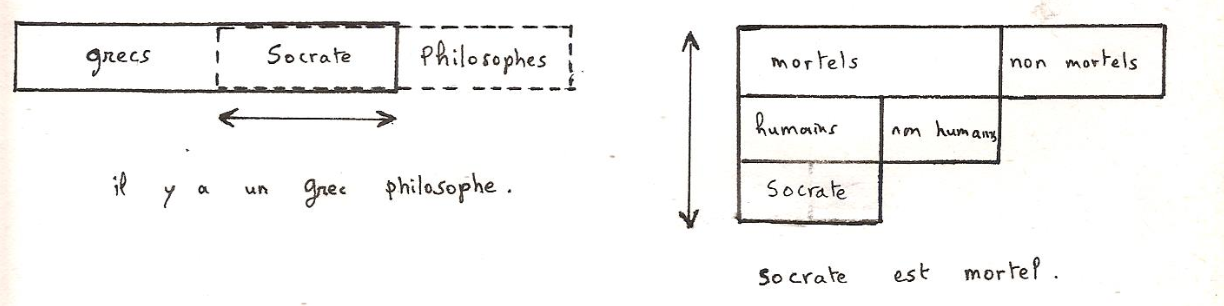
Cette origine hybride explique certainement la complication excessive et l’hypertrophie de la syllogistique, avant que la représentation graphique des relations d’inclusion due à Euler, et les progrès de la logique formelle, ne l’aient réduite à peu de chose. Pas plus que la dichotomie, le syllogisme ne découvre rien sur le monde : il clarifie et explicite des rapports contenus dès le départ dans le petit terme et le grand terme. Cependant, tandis que la dichotomie divise arbitrairement, le syllogisme rapproche, réunit des idées distinctes comme par un dynamisme interne, ce qui est, nous l’avons vu, beaucoup plus proche du processus d’invention :
« lors donc que la seule considération de deux idées ne suffit pas pour faire juger si l’on doit affirmer ou nier l’une de l’autre, l’esprit a besoin de recourir à une troisième idée, et cette idée s’appelle moyen[73] »
Le moyen terme, qui s’efface dans lá conclusion du syllogisme est donc le pivot de la méthode, parce que lié des deux côtés aux termes à rapprocher.
Par là, on peut se demander s’il n’appartient pas à cette catégorie générale des « mixtes » qu’ Albert Lautman[74], reprenant le concept de schème transcendantal de Kant – » troisième terme homogène d’un côté à la catégorie et de l’autre au phénomène » – considère comme essentiel dans l’évolution des mathématiques :
» le rôle médiateur de ces mixtes va résulter de ce que leur structure imite encore celle du domaine auquel ils se superposent, alors que leurs éléments sont déjà du genre des êtres qui naîtront de ce domaine. »
L’introduction d’un troisième terme intermédiaire apparaît donc assez naturelle lorsqu’on se propose de relier deux notions avoisinantes. Remarquons, pour conclure ce paragraphe, qu’il peut aussi se glisser, à titre de frontière, à l’interface de deux domaines que l’on désire garder séparés. Prenons par exemple la problématique du dualisme absolu esprit-matière, telle qu’elle se posait au XVIIe siècle :
- soit, par le système des causes occasionnelles, on admettait que Dieu à tout instant accordait les pensées de l’âme et les mouvements du corps (solution « par en haut » ) ;
- soit, avec Leibniz, on expliquait cette apparence d’influence mutuelle par l’harmonie préétablie des monades (solution « par en bas » );
- soit enfin avec Descartes[75], on se résignait à l’existence d’un point de contact, la glande pinéale, suspendue au centre du cerveau, et dont les menues oscillations permettaient de boucher alternativement les canaux correspondants aux diverses passions ( solution « par le milieu » ).
Il est curieux de constater comment l’intuition physique et la nécessité logique se mêlent étroitement dans le choix de cette glande : puisque les organes des sens sont doubles, et que nous n’avons qu’une seule perception sensible à la fois, il faut nécessairement qu’avant d’être transmises à l’âme, elles s’assemblent en un même point ; c’est à l’heureuse circonstance d’avoir été unique au milieu d’un cerveau dont toutes les parties sont doubles, que la glande pinéale doit d’être restée comme un des exemples les plus baroques d’introduction d’un terme intermédiaire.
L’échappée dans l’ailleurs.
Lorsqu’il semble impossible d’intercaler un terme intermédiaire, tampon, entre les deux termes d’un système binaire, et que néanmoins cette binarité, perçue comme contradiction, est jugée insupportable, l’esprit a tendance à s’évader hors de la région conflictuelle, à la recherche d’un « ailleurs » où un arbitrage, une fusion, une synthèse s’avérera possible. Nous ne nous dissimulons pas la grande diversité de ces démarches intuitives, et leur irréductibilité à un même schéma de pensée : seule les rapproche cette commune volonté d’évasion.
L’échappée « spatiale »
La contradiction doit être résolue de manière permanente, par la recherche « topographique » d’un lieu où elle perdra son caractère absolu. L’un des moyens de cette échappée est le recours à l’infini. Ainsi un des exemples de « coincidentia oppositorum » donné par Nicolas de Cues, est celui du mouvement et de l’immobilité : il suffit de considérer un corps se mouvant sur une trajectoire circulaire, à une vitesse infinie ; l’égalité des contraires est réalisée dans un monde idéal, où le recours à l’incommensurable est licite. Plus généralement, l’idée maîtresse de Nicolas de Cues semble être que les termes extrêmes d’une relation d’ordre sont « en dehors » des termes de cette relation, et par là même, assez mystérieusement, nécessairement égaux[76]. C’est donc l’ « étirement » indéfini de la contradiction qui fait apparaître son caractère contingent.
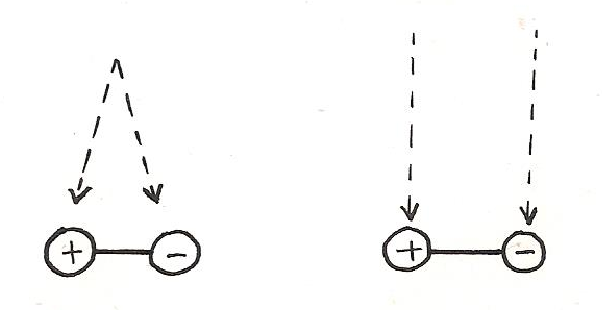 On peut également rechercher un point d’union externe, situé sur un plan »d’autant plus élevé que l’écart entre les termes est plus grand » : l’image du triangle s’impose alors, dont deux côtés sont parallèles dans le cas d’une antinomie ne pouvant se résoudre qu’en Dieu[77].
On peut également rechercher un point d’union externe, situé sur un plan »d’autant plus élevé que l’écart entre les termes est plus grand » : l’image du triangle s’impose alors, dont deux côtés sont parallèles dans le cas d’une antinomie ne pouvant se résoudre qu’en Dieu[77].
En ce point géométral,les contrariétés s’effacent, et c’est ensuite pour l’âme, selon l’expression de Giordano Bruno, « une grande et profonde magie que de tirer les contraires après avoir trouvé le point de l’union. »
Cependant, cette intuition d’un »plan supérieur » n’est pas l’apanage des seuls mystiques. Elle s’introduit par exemple en logique, dès lors qu’un processus d’abstraction est en jeu sous peine d’antinomie, il est impossible de considérer l’objet abstrait (relation, classe, fonction…) comme homologue aux termes qu’il unit, comme du même ordre : nous reviendrons sur cette notion dans Annexe III : La méthode de la diagonale et la construction de cercles vicieux. Mentionnons seulement ici, pour illustrer la puissance intuitive de cette ascension indéfinie, la magnifique image due à Lanza del Vasto[78] d’un monde comme pyramide de relations, accrochées les unes aux autres à la manière de balances oscillantes :
« le nombre de termes diminue dans la mesure où ils s’élèvent et gagnent en fixité, donc en consistance, en être La pyramide aboutit par conséquent à une seule relation, dont les autres dépendent et qui ne dépend d’aucune. »
L’échappée temporelle : la dialectique.
« Entre les aspects de la contradiction, il y a à la fois unité et lutte, c’est cela même qui pousse les choses et les phénomènes à changer » Mao Tsé Toung
Il ne s’agit plus maintenant de rechercher, où qu’il se trouve, « 1’Un original, homogène et simple, et d’où serait sortie par différentiation la multitude complexe des contraires[79]« ,mais au contraire de reconnaître le rôle moteur de la contradiction, de lui restituer sa dimension historique. Il ne nous appartient pas ici d’exposer, ne serait-ce que sommairement, en quoi consiste la ou les méthodes dialectiques, ni de déterminer dans quelle mesure le troisième terme, la synthèse, efface les deux précédents ou les confond dans une unité d’ordre supérieur. Qu’il nous suffise ici, d’un point de vue intuitif, de remarquer qu’il se situe à la fois « ailleurs », puisqu’il est d’une nature nouvelle, émergente; « au-dessus » comme le suggère le terme de Aufhebung ; mais surtout « après »: la première triade de Hegel, l’Etre, le Non-Etre et le Devenir, illustre bien ce déploiement nécessaire de la contradiction sur l’axe temporel.
Le trois triomphant.
« Le monde est parfait parce qu’il contient des corps ; le corps est parfait parce qu’il a trois dimensions ; les trois dimensions sont parfaites parce que trois sont tout ; et trois sont tout parce qu’on ne se sert pas du mot de tout quand il y a une chose ou deux, mais seulement quand il y en a trois. »
Ce raisonnement d’Aristote, cité par la Logique de Port-Royal comme exemple de sophisme, montre combien la ternarité peut être à la fois fascinante et pernicieuse. Nous l’avons vue naître, impérieuse et multiforme, dans l’idée d’un mixte, d’un terme synthétique nous avons vu se multiplier dans des pyramides dialectiques ; comme si la pensée, confrontée à la binarité seule, se trouvait bancale, déséquilibrée, contrainte à fuir vers des lieux plus stables.
Nous nous arrêterons à l’orée de cette ternarité triomphante. Car plus que du raisonnement et de la recherche intuitive, elle relève de la croyance et du mythe. Voire même du style et de la musicalité : pourquoi ces périodes temaires si fréquentes, dans une énumération, une classification, ou une démonstration ? Pourquoi attendons-nous inconsciemment, après le « toc, toc », le « et toc » péremptoire qui marque l’achèvement ? Réminiscence du syllogisme, habitude de la dissertation en trois points ? Faute de réponse, nous présenterons ci-après quelques échantillons de systèmes ternaires, voire trinitaires, dont la mise en parallèle nous semble suggestive.
Quelques divisions ternaires de l’Histoire :
| Auguste Comte | Age théologique
causes surnaturelles |
Age métaphysique
causes abstraites, scholastique |
Age positif
science |
| Korzybski | Période préscientifique
Seul compte l’observateur |
Période classique
Seul compte l’objet observé |
Période scientifique
interaction observateur-observé |
| Althusser[80] | Continent mathématique
Grèce |
Continent physique
Descartes, Galilée |
Continent histoire
Marx, matérialisme dialectique |
| L.Mumford[81] | Age éotechnique
énergies faibles |
Age paléotechnique
charbon, bois |
Age néotechnique
énergies transportables |
Quelques divisions ternaires de la nature, ou par analogie avec la nature :
| Korzybski | Végétal
relie entre elles des énergies |
Animal
en plus, relie des points de l’espace (locomotion) |
Homme
en plus, relie des moments du temps (mémoire) |
| Lupasco | matière macrophysique
homogène |
mat. vivante
hétérogène |
mat. microphysique, pensée homogène et hétérogène |
| Schleicher[82] | langues isolantes
relation et signification s’expriment de manière indifférenciée |
agglutinantes
sons exprimant la relation différents des sons signification |
à flexion |
| analogues à : | cristal | plantes | organisme animal |
| A.Virel[83] sur l’évolution de l’imaginaire: | phase cosmogénique
indifférentiation, éternel présent |
phase schizogénique
séparation du milieu, temps cyclique |
phase autogénique
être centré, se construisant lui-même. |
| analogues à : | énergie | matière inorganique | matière vivante |
Ces quelques exemples n’ont d’autre but que de montrer la complexité des analogies et des recoupements corrélatifs à la division par trois. Il semble que la considération d’une propriété ternaire, ou de trois objets liés par une même propriété, suffise à provoquer la mise en parallèle d’autres séquences apprises, d’autres modèles triadiques. L’impression de « compréhension » proviendrait de la reconnaissance de ces schèmes familiers.
Citons encore, faute de pouvoir conclure, les systèmes de deux trinitaristes avérés :
- celui du mathématicien américain Ch.S.Peirce, qui célébrait la ternarité comme le fondement logique de la Création : « la structure ternaire est si prolifique que l’on peut facilement concevoir que toutes les structures multiples de l’Univers en découlent[84]« . Peirce distinguait trois catégories :
- la primarité, existence d’une chose en elle-même : par exemple la couleur rouge, indépendamment de tout objet rouge.
- la secondarité, une chose dans ses relations avec d’autres : par exemple une pomme rouge.
- la tertiarité, deux objets mis en relation par un troisième : par exemple l’idée d’une pomme rouge.
- Lanza del Vasto et son système de triades[85], certainement l’un des plus achevés, avec ses trois triades isomorphes du Vrai, du Beau et du Bien :
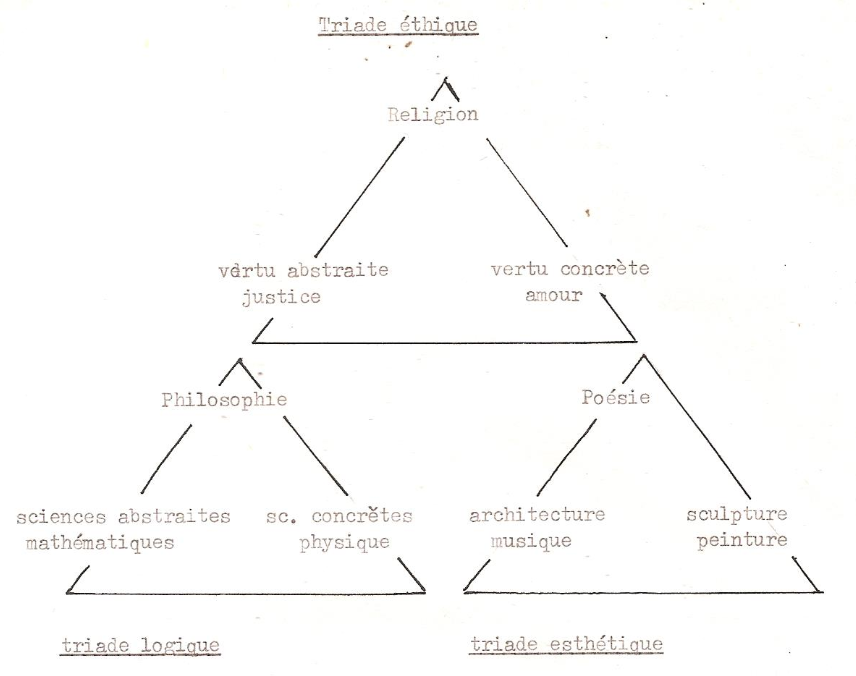
La binarité déchue. Passage au continu.
La voie que nous avons explorée jusqu’à présent, qui conduit de la binarité pure à la ternarité par adjonction d’un mixte, d’un terme transcendant ou synthétique, ne remet jamais en cause l’intuition duale originelle, ne cherche pas à contester la contradiction,mais seulement à l’amender, à en canaliser les aspects positifs par des constructions additionnelles.
Nous allons présenter dorénavant une seconde démarche, qui s’interroge avant tout sur le bien-fondé de la binarité initiale et qui conclut au non-lieu soit parce que le passage au continu entre les pôles s’avère possible, soit parce que la généralisation à l’extérieur des termes conduit à relativiser le rapport qu’ils ont entre eux. Cette seconde démarche paraît moins spéculative, moins hâtive, plus soucieuse d’expérimentation et de quantification que la première, qui sacrifie parfois la rigueur de l’analyse au prestige tragique d’une irréconciliable dualité. Si, comme le remarque J.C.Bruter à propos des mathématiques, « l’étude du discret a toujours précédé l’étude du continu », on pourrait voir ici un cas particulier de cette règle qui situerait l’intuition de la continuité à un niveau psychologique plus élaboré, en tout cas second, par rapport à celui de l’intuition dichotomique[86].
Le choix entre principes contraires et pôles de continuité, entre le oui ou non et le plus ou moins, se retrouve à tous les stades de l’évolution des connaissances. Ainsi, pour Anaxagore, s’il existe bien des contraires irréductibles, l’apparence des choses est due à l’élément prédominant : « toutes choses, si petites qu’elles soient, contiennent des portions de tous les contraires, tels que le chaud et le froid, le blanc et le noir ». Tandis que l’intellect nous présente l’eau, par exemple, comme noire en tant que noumène, nous percevons la neige comme blanche en tant que phénomène [87]. Aristote reprend cette intuition en ce qui concerne le poids : la lourdeur ou la légèreté d’un corps résulte de la proportion de terre ou de feu qu’il contient.
Cependant le grand introducteur du principe de continuité dans la pensée occidentale est bien sûr Leibniz: « la différence entre deux états (la vie ou la mort) n’est jamais que du plus au moins, un saut d’un état à l’autre infiniment différent ne pouvant être naturel.[88]« . Si ce principe de variation continue des grandeurs a contribué à son invention du calcul différentiel, de même la découverte du calcul binaire, c’est-à-dire que tout nombre est exprimable en proportion de deux contraires fondamentaux 0 et 1, a profondément influencé la physique de Leibniz, notamment sa théorie des couleurs : aucune ne serait primitive, mais toutes seraient produites par le mélange du blanc et du noir en diverses proportions, c’est-à-dire de la lumière et de l’ombre. Comme le remarque Michel Serres, opposant Leibniz à Descartes : »la loi proportionnelle du peu et du tant remplace la loi d’exclusion du tout et du rien [89]«
Durant le XVIII° siècle, tandis que les progrès des sciences de la nature tendaient à faire se rejoindre les trois règnes minéral, végétal et animal, cette intuition de la continuité devint la coqueluche de la pensée ; c’est, notamment, le « Ruban du Père Castel » du Rêve de d’Alembert:
« il n’y a aucune qualité dont aucun être ne soit participant… et c’est le rapport plus ou moins grand de cette qualité qui le fait attribuer être exclusivement à un autre »
Le débat se poursuivit en physique même, du Fay postulant l’existence de deux types contraires de fluide électrique, et Franklin expliquant la polarité par la surabondance ou l’insuffisance d’un seul et même fluide[90]. Il serait trop long de montrer comment les théories modernes de la conduction réconcilient en quelque sorte ces deux savants, tandis qu’une contrariété, pour l’instant irrésolvable, s’est instaurée ailleurs, entre particules et antiparticules. Remarquons seulement que jusqu’à un certain point, une des constantes de la méthode scientifique est justement de suspecter sous des qualités discrètes la variation d’un principe continu. Un exemple curieux nous est fourni, en biologie, par l’hypothèse de Wilhelm Ludwig[91] visant à expliquer la dissymétrie des pinces d’une espèce de homard : il suppose que deux agents D et G sont distribués dans l’organisme selon un certain champ de gradient, et tel que la concentration de ces agents varie de gauche à droite en sens inverse. L’agent dominant serait responsable de la structure de la pince.
Cependant il semble bien, en physique tout au moins, que la mécanique quantique ait sonné le glas d’une prétention universelle à la continuité. Terminons ce rapide survol en citant à l’encontre de Lupasco l’opinion d’Hermann Weyl sur le rôle unificateur de la relativité einsteinienne, cette apogée de la physique classique :
« un dualisme de la matière et du champ naquit ainsi (au cours du XIX° siècle), éther et matière formant deux essences distinctes et séparées qu’une interaction constante réunit cependant 1’une à l’autre. Puis la relativité abolit ce dualisme: la matière cesse d’apparaître comme une existence physique à côté du champ pour se ramener à ce dernier et former un produit du champ.[92]« (31)
Nous nous proposons maintenant, à travers deux exemples dans le domaine de la logique, d’examiner de manière plus précise les modalités de ce passage au continu:
L’analytique et le synthétique
Sans prendre position dans un débat de plus en plus inextricable, « dans la mesure où on tient à une séparation radicale au lieu de considérer l’analytique et le synthétique comme deux pôles reliés par tous les intermédiaires », ainsi que le juge Piaget[93], nous voudrions tenter d’en présenter les données initiales et l’évolution, qui nous semble significative du mouvement vers le continu que nous avons essayé de définir. Considérons l’énoncé « un célibataire n’est pas marié ». Il est analytique en ce sens qu’il lie deux termes dont le second est contenu » dans la signification du premier ; il résulte d’une nécessité interne aux termes en présence. Si par contre nous disons « Untel n’est pas marié », l’énoncé est synthétique en ce sens que la qualité « n’être pas marié » apporte une précision nouvelle, indépendante du premier terme.
Une distinction tranchée entre ces catégories est d’importance: ainsi par exemple, selon que l’on place le syllogisme dans l’un ou l’autre camp, on est en droit de le considérer soit comme simple moyen de liaison entre termes, soit comme authentique instrument de découverte.
Cependant, une seconde dichotomie vient se greffer en parallèle à la dichotomie analytique/synthétique celle de l’ « a priori », connaissance qui découle des seules nécessités internes de l’esprit, et de l’ « a posteriori » qui implique une expérience sur le monde. Là encore la distinction est fondamentale : le statut à attribuer aux mathématiques en découle.
Ces deux dichotomies, dont le premier terme de chacune se réfère à l’intuition de clôture sur soi, d’autonomie, et le second dénote l’ouverture vers l’extérieur, la génération d’un être nouveau, semblent assez facilement superposables. Kant s’avisa le premier que leurs frontières ne coïncidaient pas :
 Il existe donc une catégorie supplémentaire, le « synthétique a priori » dans laquelle nous pouvons par exemple classer les mathématiques : le jugement 5+7=12 comporte bien la formation d’une entité nouvelle, le nombre douze, et cependant à partir de règles inhérentes à notre seul esprit. Ainsi entre deux dichotomies absolues, formes modernes sans doute du dualisme platonicien, s’intercala une catégorie originale, dont l’influence fut déterminante au cours du XIX siècle : le 50ème axiome d’Euclide par exemple, en tant que synthétique a priori, devait être vrai dans l’absolu, sans expérimentation possible. La longue résistance aux géométries non-euclidiennes fut pleinement levée seulement lorsque la Relativité permit de déplacer, dans la catégorie des « synthétiques a posteriori », le postulat des parallèles.
Il existe donc une catégorie supplémentaire, le « synthétique a priori » dans laquelle nous pouvons par exemple classer les mathématiques : le jugement 5+7=12 comporte bien la formation d’une entité nouvelle, le nombre douze, et cependant à partir de règles inhérentes à notre seul esprit. Ainsi entre deux dichotomies absolues, formes modernes sans doute du dualisme platonicien, s’intercala une catégorie originale, dont l’influence fut déterminante au cours du XIX siècle : le 50ème axiome d’Euclide par exemple, en tant que synthétique a priori, devait être vrai dans l’absolu, sans expérimentation possible. La longue résistance aux géométries non-euclidiennes fut pleinement levée seulement lorsque la Relativité permit de déplacer, dans la catégorie des « synthétiques a posteriori », le postulat des parallèles.
Cependant, des considérations de nature sémantique contriburtent peu à peu à jeter le doute sur la suffisance de la construction kantienne. Soit l’énoncé : « un prêtre n’est pas marié » .Le considérer comme analytique ou synthétique nécessite évidemment une exacte définition du domaine linguistique de référence, et une recension complète des différentes significations du premier terme dans ce domaine. Soit donc, comme les empiristes logiques, on s’emploie à sauvegarder la distinction initiale, quitte à devoir multiplier de manière pénible le nombre de catégories ; soit au contraire on se résigne à une continuité entre analytique et synthétique, qui ôte à ces notions une grande partie de leur intérêt. Ainsi Piaget : »cette distinction n’est pas tenable, et il s’agit d’une simple illusion de perspective[94]« .
Logiques multivalentes.
La logique occidentale semble être le lieu d’élection de la pensée binaire. Certains ne se font pas faute d’opposer à son principe du Tiers-Exclu, qui met en demeure l’esprit de se déterminer entre seulement deux termes, la moindre rigidité de la pensée orientale : ainsi le bouddhisme zen admet un terme d’indifférence, le « mu », qui s’impose lorsque le contexte d’une question est trop réduit pour répondre. D’autres, impressionnés par l’étrangeté des découvertes de la mécanique quantique, ont conclu de manière plus ou moins hâtive à la caducité de la logique traditionnelle. Toute polémique en la matière apparaît désuète, devant les divers développements qu’ont inspirés aux logiciens eux-même les évidentes limitations de la logique bivalente : nous voudrions en esquisser un panorama rapide (dans la mesure où leur caractère souvent très technique se laisse pénétrer), et montrer qu’ils s’inscrivent dans le processus naturel de passage au continu que nous avons déjà observé[95].
Logique trivalente (Post, Lukasiewicz, 1920)
Cette logique reprend le vieux problème d’Aristote sur le statut à attribuer à une proposition du type « il y aura demain une bataille navale », potentiellement vraie et actuellement fausse. On considérera cette proposition comme neutre, et on introduira donc, entre le 1 et le 0 de la logique classique, une valeur de vérité 1/2 désignant cet état. Le problème est de définir pour les opérateurs logiques des tables de vérité conduisant à une structure intéressante, et permettant une axiomatisation. On aura ainsi, pour la conjonction et la disjonction :

Il y a donc extension, sans les modifier, des règles valables pour la logique bivalente. Le principe du Tiers-Exclu est remplacé par un principe du Quart-Exclu.
La structure déterminée par ces deux opérations est le « treillis de Post ». Il diffère du treillis de Boole de la logique bivalente, distributif et complémenté, par le fait que l’élément 1/2 n’a pas de complément (p est le complément de q si p et q = 0, p ou q = 1). La distributivité est conservée, ainsi que les règles de dualité entre et et ou. Cette logique s’applique notamment dans le cas de réseaux électriques possédant trois états de commutation.
Lukasiewicz a étendu cette méthode à des logiques à quatre, cinq, voire une infinité dénombrable (analogue à celle des entiers naturels) de valeurs de vérité.
Passage au continu.
Il s’agit d’attribuer à toute proposition p une valeur V(p) variant continuement dans l’intervalle S = [0, 1]. Deux voies doivent être distinguées:
1) la logique du probable (Keynes 1921, Reichenbach 1934) utilise les lois de composition arithmétiques de S. On définit ainsi :
- V(p et q) = V(p).V(q)
- V(p ou q) = V(p) + V(q) – V(p).V(q)
La « probabilité » de p est définie en fonction de ces valeurs de vérité. On a ainsi :
Prob (p et q) = Prob(q).Prob(p/q), ce dernier facteur désignant la probabilité d’avoir p, q étant réalisée. Cette logique n’est donc pas une logique intentionnelle (chaque opérateur exprimable par des tables de vérité), puisque le degré de « couplage » entre p et q intervient.
2) la logique « floue » (Zadeh) nécessite seulement que S soit un ensemble totalement ordonné. On définit deux opérations :
- V(p) ˄ V(q) = Min(V(p), V(q))
- V(p) V V(q) = Max(V(p), V(q) )
Muni de ces deux opérations, l’ensemble des V(p) est encore un treillis distributif non complémenté. Les lois de dualité entre ces deux opérations sont valables : elles correspondent au changement de V(p) en 1- V(p), soit à une inversion de l’ordre dans le segment [0,1]. En vertu de cette dualité, toute fonction de V(p) peut être exprimée sous forme d’un polynome en « ou » ou en « et », dont il existe une forme canonique (i.e. tous les monômes sont minimaux). Cependant l’énumération des formes canoniques est plus difficile qu’en logique bivalente, du fait qu’il n’existe pas de table de vérité pour permettre la simplification des expressions ; au lieu de 16 opérations binaires, on en dénombrera 166.
On constate que ces deux logiques du probable et floue se ramènent bien à la logique bivalente ordinaire, lorsqu’on restreint S à {0, 1}. Cependant la généralisation floue apparaît la plus naturelle. En effet, les valeurs logiques attribuées aux variables doivent être purement conventionnelles : il est équivalent de les noter V et F ou 1 et 0. Le passage au continu s’effectue en identifiant l’ensemble des valeurs possibles avec le segment [0, 1],mais dont les propriétés arithmétiques n’ont pas à intervenir ; seul importe le repérage mutuel des valeurs de vérité c’est à dire le caractère totalement ordonné de S.
Ainsi, par l’introduction progressive d’un troisième terme d’indifférence, puis d’autrestermes discrets, puis finalement par passage au continu se construit une « analogie » numérique qui les contraires Vrai/Faux en pôles PlusVrai/PlusFaux. Cependant, si cette généralisation, très cohérente, retrouve et développe les structures de la logique bivalente, elle en perd la clarté intuitive. Quelle est en effet l’interprétation exacte de cette quantification : probabilité, extension de la fonction caractéristique d’appartenance à un ensemble, en ce qui concerne la logique floue ?
La logique trivalente seule a donné le jour à des interprétations allant de pair avec son développement formel, afin de tourner certaines difficultés conceptuelles nées de la théorie des quantas. Nous voudrions reprendre brièvement une interprétation due à Mme Destouches-Février (1937), sous le nom de logique de la complémentarité. On sait qu’en mécanique quantique, les « questions » se posent par l’intermédiaire d’opérateurs (position, quantité de mouvement…), la réponse étant forcément une des valeurs propres (en nombre fini ou infini) de cet opérateur. Ainsi, la structure mathématique de l’opérateur permet d’exclure a priori, sans faire de mesures, toute une série de valeurs qui sont donc « absolument fausses » (A) ; la mesure permet ensuite de déterminer quelle valeur est vraie (V), les autres valeurs propres devenant dès lors simplement « fausses » (F)·
!La logique trivalente de Lukasiewicz, qui peut être considérée comme l’extension modale d’une logique bivalente, s’applique bien à cette situation :
- « 1 »= nécessaire (V)
- « I/2 » = valeur possible, mais contingente (F)
- « 0 » = absurde (A)
Cependant, l’existence des inégalités de Heisenberg fait apparaître l’impossibilité d’appliquer cette logique à toute paire de propositions expérimentales. Soit en effet les deux propositions :
- P : « la composante px (quantité de mouvement) a la valeur p0 à l’instant t0«
- Q : « la coordonnée x a la valeur x0 à l’instant t0«
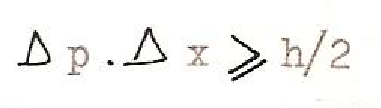 Les opérateurs p et x étant liés par la relation de Heisenberg
Les opérateurs p et x étant liés par la relation de Heisenberg
il est impossible de déterminer simultanément la valeur de vérité des deux propositions ; si P est V ou F, Q est indéterminée : on posera qu’elle est absolument fausse. Dès lors la conjonction, par exemple, sera donnée par :

La logique de la complémentarité, qui doit définir des lois différentes pour ces deux sortes de paires de propositions, n’est donc pas une logique formelle : car les opérations ne sont pas définissables indépendamment de la nature des propositions à composer.
Ce manque d’universalité a conduit à conserver, en mécanique quantique[96], les lois de la logique classique, moyennant une restriction de la « disponibilité » des propositions formulables : il suffit de poser que, tant qu’une mesure n’est pas effectuée, aucune prévision n’a de sens (non-distinction du faux-contingent et du faux-absolu).
Ces diverses tentatives prouvent qu’il est abusif de taxer la logique de manichéisme coupable, de déplorer son principe du « tout ou rien » : la dichotomie Vrai/Faux n’a rien de répressif ni de pervers, mais est seulement la rançon de l’universalité. Quant au principe du Tiers-Exclu, il est plus affaire de commodité que de dogme. Les logiques multivalentes constituent une généralisation naturelle, quoique difficile à interpréter et à appliquer.
Si donc le passage au continu est admissible en droit, il faut bien reconnaître qu’il n’épuise pas la puissance intuitive de la binarité initiale. Nombre d’auteurs ne s’en déclarent pas satisfaits (Lupasco, Abellio…) et tentent de proposer des constructions moins austères (logique du contradictoire, quaternité…), que nous renonçons à exposer dans le cadre de ce rapide survol[97].
Comme nous venons de le voir, une certaine tendance de l’esprit et spécialement de la pensée scientifique , est de combler les lacunes entre des termes qu’une première démarche avait cru séparés, en fournissant contre-exemples et intermédiaires. Lorsque cependant la binarité initiale s’avère irréductible, une itération permet de diminuer son importance relative, de dénaturer ce que le hiatus pouvait avoir de désobligeant. Cet état d’esprit nous paraît par exemple être celui de Bertrand Russell, définissant le nombre comme « classe de classe », s’interrogeant sur la construction des ensembles d’ensembles, comme si par ce double chevauchement, il était possible de résorber la distinction fondamentale de l’élément et de l’ensemble. Nous ne prétendons pas bien sûr que tout besoin de généralisation découle d’une fuite devant la binarité, mais seulement que certains cas de passage du deux au trois permettent, suivant qu’ils s’effectuent plus ou moins facilement, de tester la nature exacte d’une binarité que l’approche directe est impuissante à réduire. Ainsi, lorsque le même Russell s’attache à définir les propriétés d’une relation ternaire, par exemple « a est entre b et c [98]» (37), par rapport à celles des deux relations binaires « a ≤ c » et « b ≤ a », c’est avant tout pour essayer de comprendre la remarquable hégémonie de celles-ci, et les limites de la pensée relationnelle.
Un problème similaire s’est posé en mathématiques, à propos des nombres complexes, qui réalisent en une seule entité la synthèse de deux variables réelles (z = a + ib). Peut-on imaginer, sous une forme comparable, la synthèse de trois ? Hamilton, par la découverte des quaternions, a montré que pour conserver la structure de corps, la généralisation devait comporter quatre termes .(q = a + iu + jv + kw, avec ij=k, jk=i, i2 =j2 =k2 ). Le nombre q permet alors de décrire une rotation dans l’espace, de même que le nombre z décrivait une rotation dans le plan. Mais il a fallu au passage renoncer à la commutativité de la multiplication.
Nous voyons ici comment une volonté de généralisation se heurte à une contrainte « spatiale », indépendante de cette volonté. D’autres exemples sont aisés à trouver : ainsi, tandis que dans le plan toutes les formes de polygones réguliers sont possibles, dans l’espace ne peuvent exister – on connaît les implications philosophiques cette situation, de Platon jusqu’à Kepler – que cinq polyèdres réguliers. Le problème obsessionnel de la trisection de l’angle, à l’aide d’une règle et d’un compas, fournit un autre exemple de résistance à la généralisation, dû à une contrainte algébrique cette fois.
Ces exemples épars ne prouvent rien, mais on peut espérer qu’une étude systématique de ces transitions du binaire au ternaire aiderait à distinguer ce qui revient à 1’esprit (aptitude à la généralisation indéfinie, mais difficulté à concevoir des relations entre plus de deux objets) et ce qui revient au monde.
La dualité et ses paradoxes.
Nous nous sommes intéressés aux relations entre binarité et ternarité, entre le deux et le continu, entre le deux et le multiple. Mais pas encore au passage entre lle deux et le un.
 Un exemple en physique est le passage continu du monaire au binaire dans le phénomène de Van der Pol : d’un cycle non marqué, on passe progressivement à un cycle d’hystérésis à deux paliers[99].
Un exemple en physique est le passage continu du monaire au binaire dans le phénomène de Van der Pol : d’un cycle non marqué, on passe progressivement à un cycle d’hystérésis à deux paliers[99].
Ce passage revêt souvent un caractère paradoxal dès lors que les propriétés d’additivité auxquelles nous nous attendons ne sont pas respectées.
D’un point de vue logique, il semble que ceci tienne à la difficulté de concevoir une relation d’idempotence du type « A = A ou A », tandis que nous sommes habitués à des relations du type « A = A/2 + A/2 ». Un paradoxe célèbre, dirigé soit contre l’idée de substance infinie, soit contre l’idée de substance divisible, est basé sur cette incompréhension de l’idempotence, la division en deux parties infinies conduisant à l' »absurdité »: « infini = infini + infini [100]».
Mais ces paradoxes dépassent largement le domaine de la seule logique. Ainsi, un aimant coupé en deux redonne deux semblables, mais plus petits ; un ruban de Moebius, un semblable deux fois plus long. Le caractère énigmatique n’apparaît bien sûr que si l’on se concentre sur les caractères de ressemblance, au détriment des différences de dimension : on a alors « aimant = aimant + aimant » ; « ruban / 2 = ruban ».
Combien le cas de coupures non additives est étranger à notre intuition immédiate, est illustré par la mésaventure du biologiste H.Drietsch qui, découvrant qu’en divisant l’oeuf d’oursin en deux blastomères, on obtenait deux gastrulas complètes (quoique plus petites) et non deux moitiés, expliqua le phénomène par l’intervention d’entéléchies renouvelées d’Aristote, qui ruinèrent sa réputation scientifique[101]. Le fait que ce passage entre deux et un soit analogiquement lié aux grands mythes de la reproduction sexuée ou pas scissiparité ajoute encore à l’obscurité de l’intuition. En outre, la moindre ressemblance entre la partie divisée et le tout ramène inévitablement aux modèles troublants de l’emboîtement et du multiple dans l’un.
Nous n’en dirons pas plus sur ces exemples où l’intuition se brouille, hésitant entre plusieurs figures . Il nous semble plus positif de dégager, corrélativement, la notion de dualité. Dans l’annexe II, nous illustrons par des exemples mathématiques cette figure, liée aux idées de symétrie, et d’inversion d’un sens de parcours. Qu’il nous suffise ici d’invoquer la double dichotomie de La République de Platon, dans laquelle 1’intuition duale est manifeste :

Cette hiérarchie très subtile est basée sur une série de proportions, à deux niveaux : les reflets sur les objets sont aux objets réels ce que les mathématiques sont à la dialectique, mais aussi ce que la totalité du monde visible est elle-même au monde intelligible. Ainsi, chaque unité se dédouble en deux moitiés symétriques, dont l’ensemble à son tour est symétrique d’un autre.
Telles sont, nous semble-t-il, les caractéristiques de la dualité : le monde est séparé en deux moitiés symétriques, se réfléchissant l’une l’autre. Cependant, l’une des deux suffit à reconstituer le tout, et la dualité s’abolit dès lors que nous parvenons à nous convaincre que le reflet coïncide avec l’original.
Le circulaire et le linéaire.
Zeus : « je m’en vais en effet, poursuivit-il, couper par la moitié chacun d’eux… ainsi ils marcheront tout droits sur leurs deux jambes »
Le mythe du Banquet, où l’on voit les hommes déchus de leur perfection circulaire par une division ignominieuse, voire menacés d’aller à cloche-pied s’ils s’obstinent dans leur orgueil, n’est qu’une boutade d’Aristophane. Mais le parallélisme unité/dualité et circularité/linéarité qu’il suggère ne serait-il pas plus profond ? Dans la physique aristotélicienne, les éléments dont sont composés tous les objets sublunaires bougent en ligne droite vers leur place propre, feu et air vers le haut, terre et eau vers le bas. Car
« les éléments ont des contraires, dont ils s’éloignent par leur mouvement ; et tout mouvement en ligne droite …implique l’existence d’un tel contraire. Mais les corps célestes se meuvent en cercle, c’est ainsi que leur mouvement prouve qu’ils sont sans contraires. Et ce qui n’a pas de contraire doit être exempt de génération et de corruption physique puisque, selon Aristote, tous les objets procèdent de leur contraire et sont à nouveau corrompus en leur contraire.[102]« (41)
 Dans ce passage de St Thomas d’Aquin se trouvent synthétisées nombre de figures intuitives que nous avons rencontrées jusqu’ici :
Dans ce passage de St Thomas d’Aquin se trouvent synthétisées nombre de figures intuitives que nous avons rencontrées jusqu’ici :
- mouvement linéaire en sens inverse entre les contraires, qui les oblige à chaque extrémité à inverser leur nature afin que la compensation soit possible ;
- unité et permanence de l’objet en mouvement circulaire.
Le schéma linéaire suggère l’idée d’un choc, d’une compétition à mi-chemin, tel un équilibre chimique ; le schéma circulaire illustre la conservation de soi-même à travers les transformations, à l’image d’un cycle thermodynamique.
En termes mathématiques, la droite est homéomorphe au cercle privé d’un point. C’est cette coupure qui est fondamentale, faisant apparaître deux lèvres que toutes les tentatives de coïncidence des contraires se devront de rapprocher.
C’est cependant transposé dans le domaine temporel que ce schématisme s’est vu le plus souvent développer. Nous n’entrerons pas dans la casuistique de l’histoire cyclique ou linéaire[103]. Signalons simplement que Michel Serres a tenté de démontrer[104] que seuls six modèles géométriques du progrès étaient possibles, par composition de mouvements circulaires et linéaires :
« la droite figure un temps monodrome et un progrès accumulatif illimité ; ou, inversement, une décadence continue, une constante régression. Le cercle, à son tour, est figure de stabilité globale devenir cyclique, il combine un progrès temporaire et une régression égale au progrès, mais en sens inverse[105] ».
Mais revenons désormais sur le mouvement dans l’espace, car le schématisme linéaire / circulaire y induit des difficultés d’ordre logique dont nous voudrions faire état.
C’est encore vers Aristote que nous nous tournerons d’abord, dans sa preuve classique de l’existence du « moteur immobile ». Tout mouvement impose la présence simultanée d’un moteur, d’un mobile et d’un intermédiaire qui participe de l’un et de l’autre. Mais la chaîne causale ne peut être infinie, ce qui serait absurde. Elle doit avoir un bout : si cet ultime moteur est mobile, c’est donc qu’il se meut lui-même, ce qui est absurde. Il faut donc que ce moteur. soit immobile.
Ce qui nous semble significatif ici, c’est que nous sommes mis en demeure d’échapper à deux types de prétendues absurdités : la première tenant une propagation linéaire indéfinie, la seconde résultant d’un « noeud » dans la chaîne causale, perçu comme un cercle vicieux.
Un autre exemple typique de cette alternative est le raisonnement de Gassendi prouvant l’impossibilité du plein[106] :
s’il n’y avait pas de vide, pour que A se meuve, il faudrait qu’il prenne la place de B. Ainsi :
- soit nous aurions une régression à l’infini, absurde (B → C, C → D, …) ;
- soit il faudrait supposer un bouclage de la chaîne, à un certain point.Mais pour que A se meuve, il faut auparavant que E se soit déplacé, et réciproquement : on a donc un cercle vicieux
 Descartes, retournant ce raisonnement et partant au contraire du présupposé de 1′ »horreur du vide » en déduit que « dans chaque mouvement il doit y avoir tout un cercle ou un anneau de corps qui se meuvent ensemble[107]« . La théorie des tourbillons, et des lacunes entre les sphères de matière immédiatement compensées par des « raclures » malléables, découle directement de cet argument.
Descartes, retournant ce raisonnement et partant au contraire du présupposé de 1′ »horreur du vide » en déduit que « dans chaque mouvement il doit y avoir tout un cercle ou un anneau de corps qui se meuvent ensemble[107]« . La théorie des tourbillons, et des lacunes entre les sphères de matière immédiatement compensées par des « raclures » malléables, découle directement de cet argument.
Il est remarquable de voir comment à travers ces trois réflexions sur le mouvement, de parti pris et de conclusions radicalement différents, la même alternative nous est finalement imposée entre régression à l’infini et cercle vicieux. Combien ces deux figures sont intimement liées, l’esprit n’échappant à l’une que pour se soumettre à l’autre, c’est ce que nous allons essayer de montrer en approfondissant quelque peu ces deux notions.
Sous le nom de diallèle, le cercle vicieux fut élevé par les sceptiques au rang de trope, c’est à dire de construction logique capable d’imposer à la pensée la suspension de jugement : il consiste à remarquer que « tout ce qui sert à prouver une proposition a besoin pour être prouvé de cette proposition elle-même ». L’existence de diallèles démontre pour les sceptiques 1’impossibilité d’une connaissance certaine, de même que pour Kant, l’existence des antinomies proclamera la vanité de toute métaphysique déductive.
Prenons deux exemples de diallèles tirés des Esquisses Pyrrhonniennes de Sextus Empiricus, oeuvre où la pensée, avec un parti-pris évident, est constamment placée entre ces Charybde et Scylla que sont la régression et le cercle :
- faut-il accorder la vérité aux choses sensibles, aux concepts, ou aux deux ? Soit une chose sensible ; pour la confirmer, nous avons besoin ou bien d’une autre chose sensible (impossible, car régression), soit d’un concept. Mais ce concept lui-même nécessite une chose sensible ou un concept pour être prouvé, d’où un cercle. (I, XV)
- « il fait clair »(A) est signe qu’ « il fait jour »(B). Mais il est impossible de déduire B de A sans avoir auparavant induit A de B. Le signe et le phénomène sont deux choses corrélatives, ne peuvent être saisies que simultanément : dès lors, le signe perd tout intérêt, ne « révèle rien » de la chose qui n’ait été précédemment connu. Il faut donc conclure à son « absurdité ». (II, XI)
Comme dans la démonstration de Gassendi,le cercle vicieux est avant tout ici question d’antériorité, de préséance ; la simultanéité, seule échappatoire, est conçue comme perte de sens, puisqu’elle abolit toute distinction entre les termes.
Dans ce diallèle épistémologique, entre ces deux protagonistes que sont le monde et sa représentation, l’esprit est conduit à tourner perpétuellement sur lui-même à la recherche d’un terme premier qui se dérobe, tel le serpent mythique ouroboros 1’autophage[108] (47)
Un autre diallèle, plus terrifiant peut-être parce que plus intime, est lié au pouvoir de thématisation de l’esprit, à sa capacité de prendre pour sujet d’une pensée une pensée elle-même. Alors, le cercle vicieux ne révèle plus seulement la vanité d’une connaissance certaine, mais dénie au sujet pensant lui-même toute réalité stable. C’est le paradoxe du « moi en spirale », selon l’image d’A.Koestler[109]:
 Mais qui prouve que la spirale se referme vers un « je » asymptotique ? Ne faut-il pas craindre plutôt, là encore, la linéarité d’une régression à l’infini ?
Mais qui prouve que la spirale se referme vers un « je » asymptotique ? Ne faut-il pas craindre plutôt, là encore, la linéarité d’une régression à l’infini ?
Aussi Plotin, contre Aristote qui définissait Dieu: la « pensée de la pensée », interdit le dédoublement du moi cogitant : penser ne se distingue pas de « penser que je pense ».
Un argument plus convainquant que ce monisme universel pourrait être celui du rasoir d’Occam, de la simplicité maximale : ainsi Husserl est amené à établir une distinction unique, sans régression, entre ce qu’un acte contient à titre de partie réelle et ce qu’il met en représentation idéelle. Car sinon
« la copie entendue comme un élément réel dans la perception, conçue elle-même comme réalité naturelle psychique, serait à son tour une réalité naturelle, réalité qui fonctionnerait comme image pour une autre. Or cela ne se pourrait que grâce à une conscience de copie, au sein de laquelle quelque chose devrait d’abord.apparaître une fois, et ainsi nous aurions une première intentionnalité ; mais ce quelque chose à son tour fonctionnerait dans la conscience comme objet-image pour une autre chose, et il faudrait alors recourir à une deuxième intentionnalité fondée sur la première .Or il n’est pas moins évident que chacun de ces deux modes de conscience requiert déjà la distinction entre objet réel et objet immanent, et ainsi recèle le même problème que celui que sa construction devait résoudre.[110] ».
Cependant, sous l’influence de la cybernétique, les idées de rétroaction et de régulations ont entraîné une interprétation nouvelle du cercle vicieux, moins éprouvante pour l’esprit. Ainsi Edgar Morin, à propos du Cogito :
 Cette découverte d’un rôle créateur du cercle vicieux détermine chez cet auteur une profession de foi enthousiaste :
Cette découverte d’un rôle créateur du cercle vicieux détermine chez cet auteur une profession de foi enthousiaste :
« Briser la circularité, éliminer les antinomies, c’est là précisément retomber sous l’empire du principe de disjonction/simplification auquel nous voulons échapper. Par contre, conserver la circularité, c’est refuser la réduction d’une donnée complexe à un principe mutilant, c’est refuser l’hypostase d’un concept-maître.le discours linéaire avec point de départ et terminus, c’est refuser la simplification abstraite.… il faut passer du cercle vicieux au cercle vertueux [111]».
Nous revenons plus longuement, dans l’annexe III, sur cette figure du cercle vicieux dans les sciences formelles (mathématiques et logique). Concluons ce paragraphe par un dernier exemple du parallélisme linéarité/circularité et dualité/unité qui a le mérite de présenter la construction délibérée d’une analogie suivant ces schémas : il s’agit de la modélisation par R. Thom, dans le cadre de la théorie des catastrophes, du comportement de prédation. La difficulté provient du caractère évidemment irréversible du processus, qui doit pourtant se répéter, devenir cyclique, afin de maintenir la stabilité métabolique du prédateur [112].
Le modèle utilisé est la catastrophe de Riemann-Hugoniot (la fronce), dont la projection dans le plan des deux paramètres de contrôle a l’allure ci-dessous :
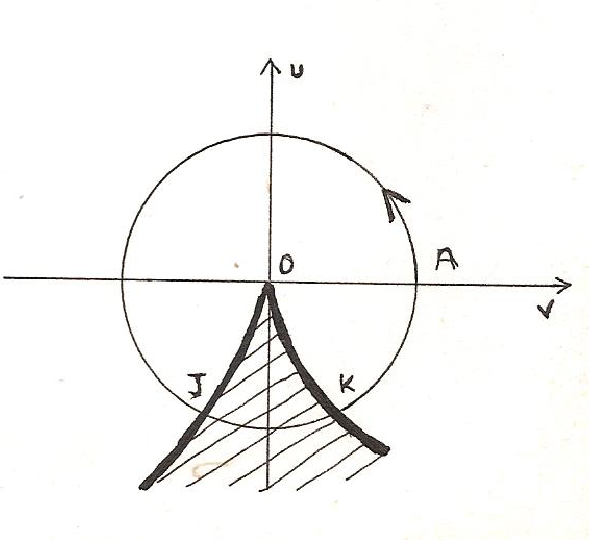 Sans chercher à pénétrer la signification mathématique précise de ce schéma, retenons simplement qu’il décrit l’évolution d’un processus à singularités, tel que le passage de la partie hachurée à la partie non- hachurée corresponde au passage entre un processus à deux « actants » et un processus à un seul actant.
Sans chercher à pénétrer la signification mathématique précise de ce schéma, retenons simplement qu’il décrit l’évolution d’un processus à singularités, tel que le passage de la partie hachurée à la partie non- hachurée corresponde au passage entre un processus à deux « actants » et un processus à un seul actant.
Considérons donc un parcours circulaire coupant cette figure en deux points J et K. Deux interprétations de ce parcours sont possibles:
- il y a deux actants entre J et K. Alors,un prédateur P décrivant la circonférence à partir de K devient en J la proie d’un autre prédateur P, et ainsi de suite. On obtient une image de la « pyramide écologique », d’une hiérarchisation pouvant se propager à l’infini. C’est l’interprétation duale et linéaire du modèle.
- il y a un seul actant, mais soumis à des transformations périodiques. Si l’axe v représente l' »énergie » du prédateur, on constate que de A en B cette énergie diminue; c’est la faim. Au minimum de v, le prédateur, obnubilé par sa proie, s’assimile mentalement à elle, s’aliène en son image ; il « devient » proprement sa proie. En J, reconnaissant une proie extérieure, il projette sur elle cette image, et redevient prédateur. De J en K, c’est la poursuite ; en K, la capture. Là, il y a fusion entre prédateur et proie, réduits à un seul actant. C’est la digestion, l’énergie augmente, puis le cycle recommence.
Si acrobatique que puisse paraître cette seconde interprétation, magnifique métaphore ou véritable modèle, elle traduit bien la volonté de privilégier l’unité ( évolution à l’intérieur d’un Même, quitte à introduire la dualité affaiblie de l’être et de sa représentation ) et la circularité paradoxale, dans l’assimilation cyclique du prédateur et de sa proie.
Ainsi se renouvelle et culmine en complexité la vieille alternative sceptique.
![]()
Annexe I : La monade et ses avatars
A la monade, dans l’oeuvre même de Leibniz, est associé un grand nombre de figures géométriques, dont nous avons mentionné par ailleurs les plus frappantes : point, étoile, noeud d’un réseau …). Michel Serres, en les prenant pour point de départ de sa brillante reconstruction de l’édifice leibnizien, a montré la richesse de ces représentations imagées et la complexité de leurs articulations. Dans ce vaste corpus de métaphores, tout ceux qu’a influencés la Monadologie n’ont pas manqué de puiser. Ainsi, on pourrait noter par exemple l’imprégnation du style de Cassirer par des images telles que le point focal, le point de vue, l’intersection de faisceaux, et plus précisément sa conception du symbole comme une sorte de monade « flottante ». Cependant, il nous a semblé intéressant, dans cette annexe, de dépasser le niveau de la simple figure, et d’étudier la monade véritablement comme modèle. Après en avoir esquissé les caractéristiques primordiales, il nous sera facile de présenter quelques exemples où l’application de ce modèle à des domaines scientifiques s’est révélée féconde, ainsi que certains cas où semble s’être produit une réincarnation spontanée de cette intuition monadique.
Origines de la monade leibnizienne
Giordano Bruno, dans son De Triplici Minimo a été le premier à rassembler, comme fondement d’un système, les trois images élémentaires de la monade[113] :
- image arithmétique (le chiffre 1), en relation avec la Science de Dieu ;
- image géométrique (le point), en relation avec la Science de l’Ame ;
- image mécanique (l’atome), en relation avec la Science de l’Univers.
Il semble bien que la monade leibnizienne tire son origine de trois inspirations similaires, bien qu’on ne puisse aucunement la réduire à l’une d’entre elles :
- plutôt que le chiffre I, les nombres premiers, sans parties par rapport à la division, et qui engendrent la totalité des entiers par agrégation de facteurs ;
- le point en tant que centre, géométral, foyer, étoile rayonnante, qui symbolise la liaison de l’Un et du Multiple ;
- 1’atome, au sens de substance indivisible, close sur elle-même, qui permet également par agrégation de reconstituer la diversité des corps.
Mais la monade leibnizienne, synthèse et abstraction de ces trois sources, représente un modèle d’une originalité radicale.
Caractéristiques du modèle monadique
- 1) La monade se situe ailleurs, dans un espace métaphysique inaccessible à 1’observation. Aussi, elle est pour nous sans étendue, sans figure et sans parties.
- 2) Elle est éternelle, sans transformation ni corruption possible. Car elle n’a ni trou ni porte » par où communiquer avec les autres monades.
- 3) le monde monadique est « dense » dans notre monde : « Il y a des âmes partout » :
- 4) La monade n’a d’être qu’en tant qu’elle perçoit et qu’elle représente le monde. Cette fonction purement spirituelle lui confère un espace et un temps particuliers :
- spatialement, elle est liée à tout l’univers monadique, qu’elle résume en elle :
« or cette liaison et cet accommodement de toutes les choses créées à chacune, et de chacune à toutes les autres, fait que chaque substance simple a des rapports qui expriment tous les autres, et qu’elle est par conséquent un miroir vivant perpétuel de l’univers[114] ».
Cette multitude de miroirs constitue l’espace perspectif de la vision divine :
« comme une même ville regardée de différents points de vue parait toute autre, et comme multipliée perspectivement ; il arrive de même que par la multitude infinie des substances simples, il y a comme autant de différents points de vue qui ne sont pourtant que les perspectives d’un seul, suivant les différents points de vue de chaque monade[115] ».
- temporellement, elle est douée de mémoire totale :« ce qui est arrivé une fois à l’âme lui est éternellement imprimé[116]« , et possède comme un pressentiment confus de toutes les perceptions futures.
- 5) La fermeture de chaque monade sur son espace intérieur (pas de communication des substances) et la nécessité de leur « conspiration universelle », impose la doctrine de l’harmonie préétablie, chaque monade étant un mécanisme, remonté de toute éternité, qui joue en accord avec les autres sa propre scénographie, sa propre représentation du monde :
« chaque monade a reçu une loi particulière, elle n’est qu’une variation de la loi générale qui règle l’univers[117] ».
- 6) La diversité du monde, composé uniquement de monades, impose que celles-ci se différencient de manière intrinsèque, suivant le caractère plus ou moins confus de leur perception du monde. Au stade le plus élevé, la monade n’est autre que l’Ame, 1″entélechie » associée à un être vivant.
- 7) La monade – mais ce point est plus obscur – semble répondre à une nécessité dynamique ; en effet, le mouvement doit être une propriété intrinsèque des corps, inscrite au dedans d’eux : car sinon, tout mouvement ne serait que la simple transposition d’un Même, et se réduirait, d’après le Principe des Indiscernables, à l’immobilité.
Reprenons ces divers points de manière plus synthétique
- les points I) et 2) se réfèrent à la nature « corpusculaire » de la monade, et notamment à sa clôture radicale. (figure correspondante : la sphère.)
- les points 3) et 4) définissent les modalités de la conjugaison du multiple et de l’un, (figure du réseau), et plus précisément de la réflexion du multiple dans l’un (figure de l’étoile, du point géométral). Ainsi que le souligne A.Lautman[118] (6), celle-ci repose sur « la réduction des rapports que la monade soutient avec toutes les autres monades en propriétés internes, enveloppées dans l’essence de la monade individuelle ». C’est cette réflexion de l’extrinsèque dans l’intrinsèque qui semble la propriété capitale de la monade. Il faut semble-t-il en distinguer deux phases :
- dans une première phase, la monade, passive, est un miroir du monde, un point de vue c’est 1’aspect perspectif de la monadologie.
- le point 5) évoque la seconde phase: la monade, active, joue sa propre vision du monde, conformément à la loi qui est inscrite en elle : elle est proprement un automate.
- les points 6) et 7) sont des conséquences du Principe des Indiscernables. Le premier point manifeste la nécessité d’un principe différenciateur entre monades appartenant à des corps « macroscopiques » différents : car d’une multiplicité d’individus identiques ne pourrait pas émerger la diversité des choses observables. Le second point tient, lui aussi,à l’explication du « macroscopique » par le « microscopique » un effet, énigmatique à notre échelle (le mouvement) doit pouvoir s’éclairer en lui supposant des agents cachés.
Après ce rapide inventaire des propriétés monadiques, nous pouvons essayer d’analyser quelques exemples de systèmes se rattachant plus ou moins directement à ce modèle.
L’éon de J.E. Charon
Si, assez anachroniquement, nous commençons par exposer la très récente oeuvre métaphysique de ce physicien[119], c’est qu’elle nous semble présenter des analogies presque point par point avec le modèle leibnizien. La distinction tranchée, dans l’oeuvre de J.E. Charon, entre la partie purement scientifique où est exposée sa théorie de la Relativité Complexe, et la partie plus philosophique où se développe une conception néognostique du monde nous autorise à nous limiter à cette dernière, sans porter de jugement sur le bâti théorique qui l’étage. Cette distinction s’opère d’elle-même par les termes, lorsque l’électron se transforme en « éon ».
La Relativité Complexe postule un dédoublement des quatre axes de notre espace-temps, chacun en une partie réelle et une partie complexe.Il se crée ainsi un deuxième monde, qui est à notre univers ce que le dedans est au dehors. Une autre image est celle de 1’Océan : dichotomie entre matière -dans notre monde – et esprit – dans le monde complexe – les électrons étant comparables à de « petites bulles d’air » qui flottent surface des eaux[120]. Si l’électron appartient à notre monde par ses effets (champ électrique,masse…), son caractère ponctuel, évanescent, prouve bien que sa réalité est « ailleurs » : dans le dedans de l’univers, il est une « sphère pulsatrice à mémoire cumulative ». Clos sur lui-même par un mécanisme d’effondrement gravifique comparable à celui des trous noirs, il contient un gaz de photons très énergétiques, soumis à un temps propre périodique, et qui constitue proprement le substrat de l’esprit. Ajoutons que bien qu’il puisse être créé ou annihilé dans des circonstances exceptionnelles, l’électron doit être considéré comme éternel.
Ainsi l’électron charonnien récapitule de manière frappante les propriétés « corpusculaires » de la monade. Le panpsychisme est retrouvé de manière évidente, puisque tout corps résulte d’une combinaison réglée d’électrons, ou d’éons, et les grands courants qui parcourent et bouleversent la matière assurent le brassage de leurs expériences propres, et la vaste solidarité de l’univers. Car si l’éon, au départ, est une « tabula rasa » vide d’informations, il retient ensuite comme des « paysages » des divers milieux où il a baigné[121], qui constituent la partie inconsciente de notre psyché, la partie consciente consistant uniquement en ce que les éons qui nous constituent ont mémorisé depuis notre naissance.
Il nous faut maintenant nous pencher sur ce mécanisme de la mémorisation, qui est le principal point de divergence avec la Monadologie alors que chez Leibniz, les monades sont incommunicantes entre elles, en dialogue seulement avec Dieu, les éons de Charon sont mutuellement liés par des « échanges de photons virtuels ». Ainsi que M. Serres l’a montré[122], l’harmonie préétablie chez Leibniz correspond à une exigence d’économie de relations, à un principe de simplicité maximale. Chez Charon au contraire, un foisonnement d’interactions assure l’accord instantané des éons, et l’harmonie se construit sans plan préétabli. Cette marche vers l’harmonie croissante est à sens unique car l’espace intra-éonique étant à néguentropie croissante, aucune perte d’information n’est possible.Le mécanisme, d’ailleurs, est décrit avec un luxe de précisions par addition d’états de spin, les photons internes se corrèlent avec les photons d’un autre électron, et le codage de l’information s’effectue de manière binaire (spins positif ou négatif), ce qui amène l’auteur à supposer, d’ailleurs, que l’électron a suggéré à l’homme le principe de l’ordinateur[123]. On connaît 1’importance du calcul binaire pour Leibniz : image symbolique de la création divine, composée de néant (0) et de tout (1); il est remarquable de retrouver chez Charonune telle convergence de « style » : ainsi, l’image du « treillis de Boole »de la Connaissance », qui unit le 0 (le moi) au 1 (1’Etre, Dieu)[124].
Pour terminer ce long parallèle, signalons qu’un principe de différentiation existe également chez Charon : « c’est le niveau de conscience de chacun des éons individuels participant à un organisme qui s’élève avec la complexité ». On passe ainsi du végétal – à l’animal et à l’homme, la part de l’Esprit augmentant toujours (néguentropie croissant) jusqu’à un point oméga renouvelé de Teilhard de Chardin.
Bien que cette perspective évolutionniste soit absente de la monadologie leibnizienne, on ne peut qu’être frappé par l’ensemble des convergences qui se manifestent entre la monade et l’éon. Il semble cependant qu’il s’agisse moins d’une influence leibnizienne directe que de la redécouverte,à partir des mêmes intuitions fondamentales, d’un modèle similaire.
Les exemples que nous allons maintenant présenter ne révéleront pas un parallélisme aussi complet, reprenant ou développant plutôt tel ou tel aspect de la monadologie.
La monade comme point de vue.
On ne peut bien sûr invoquer la monadologie à propos de toute construction se référant à une mise en perspective. Les exemples suivants manifestent cependant une inspiration monadique explicite :
- selon Humbold, « ce qui distingue les langues, ce ne sont pas les sons et les signes,mais les visions du monde elles-même ». Cassirer commente ainsi cette réflexion : « d’une manière tout à fait semblable (à la monade), chaque langue singulière devient un de ces points de vue individuels et la totalité de ces perspectives constitue le seul aspect possible pour nous d’objectivité[125] » .
- la construction logique de l’objet, par Russell, est ouvertement inspirée de la Monadologie. Constatant que toute chose est avant tout le faisceau des perceptions que nous en prenons suivant différents points de vue, et que son existence indépendante est assurée par la continuité entre ces diverses perceptions, il identifie l’objet avec la « classe de ses apparences ». Le monde matériel est alors défini de manière purement externe, comme un monde de perspectives[126].
la vision einsteinienne du monde, enfin, en attribuant à chaque observateur une indépendance radicale (critique de la simultanéité), l’accord entre les différentes perceptions étant réglés par les grands principes d’invariance, a pu faire dire à M.Merleau-Ponty :« nous retrouvons donc, d’une certaine façon, la monade de Leibniz, plus la communication effective des monades, la géométrie moderne et le concept de l’invariance, de quoi transformer en théorie mathématique une construction métaphysique[127]« .
La monade comme Multiple dans l’Un
- la manière la plus radicale de concentrer le Multiple dans l’Un consisterait à décrire les propriétés de l’espace (multiplicité virtuelle de positions) en termes de propriétés intrinsèques à un objet qu’il contient. Dans une analyse que nous ne tenterons pas de résumer, A.Lautman[128] montre comment on peut retrouver cette volonté dans les théorèmes de dualité de Poincaré, en Topologie « le polyèdre jouit ainsi de certaines des propriétés de la monade leibnizienne » ; en effet, les nombres de Betti d’un complexe Q qui servent à le caractériser, sont reliés aux nombres de Betti de l’espace complémentaire Rn – Q par une formule duale (voir annexe II) qui « permet de prévoir à l’avance le résultat de cette action de Q sur R (1’introduction d’un complexe au sein d’un espace change les propriétés topologiques de cet espace par la connaissance de la structure propre de Q »… « Le terme même d’analysis situs, dû à Leibniz, exprime bien cet espoir de déterminer ce qui concerne la « situation » par une « analyse » des propriétés internes de la figure ».
- cependant, au-delà du niveau de l’analogie, certains auteurs n’hésitent pas à attribuer à la monade un statut de véritable modèle, encore valable pour la science d’aujourd’hui. Ainsi ce théorème », énoncé par I.Prigogine et I.Stengers[129] : « tout système intégrable admet une représentation monadique ». Résumons leur argumentation: tout au long du XIX siècle, la dynamique s’est attaché au problème du choix de variables canoniques adéquates pour décrire un système d’objets en mouvements (la position et la quantité de mouvement par exemple). Par un changement approprié de ces variables, on peut en effet dans certains cas transformer l’expression de l’hamiltonien H (somme de l’énergie potentielle et de l’énergie cinétique du système) en une expression où l’énergie potentielle, qui exprime les interactions entre objets, n’apparaît plus. Le système d’équations est alors facilement résoluble, car on obtient :
« un ensemble d’unités évoluant en mouvement pseudo-inertiel, sans interactions les unes avec les autres. Chaque « unité monadique » n’est plus déterminée dans chacun de ses mouvements par les interactions dans l’agrégat, chacune déploie sa propre loi pour son propre compte, seule dans un système dont elle est intrinsèquement un reflet puisque sa définition même le suppose et le traduit dans tous ses détails »
- le même problème se retrouve en mécanique quantique, lors de la diagonalisation de l’hamiltonien dans une base de fonctions propres : « l’état stationnaire des électrons orbitaux (théorie de Bohr) constitue l’exemple-type d’état monadique ». En effet, les électrons se trouvent en quelque sorte isolés dans leur espace propre, chacun cependant « résumant » l’état du système complet puisque la diagonalisation. dépend de l’ensemble du système[130]. Ajoutons que depuis Poincaré (démonstration de la non-intégrabilité d’un système de trois corps en interaction gravitationnelle), la notion de « système monadique » a perdu toute généralité en physique. Cette notion épistémologique se dégage donc au moment même où, dans l’esprit de ses introducteurs, elle doit être dépassée.
- des analogies monadiques ont été tentées au sujet de théories physiques récentes, qui mettent en question la notion de particule indépendante. Dans un article intitulé « la monadologie de Chew[131]« (physicien auteur d’une de ces théories), G. Gale s’attache à montrer – şi tant est que la difficulté et la nouveauté des matières traitées permettent une analyse précise – que le « bootstrap des hadrons » peut s’interpréter en termes monadologiques. Selon cette théorie,les hadrons devraient être regardés comme des particules composées d’autres particules, chacune figurant à son tour « paradoxalement » parmi les composantes de ses propres composantes : « chaque particule aide à engendrer d’autres particules, qui l’engendrent en retour ». Ainsi, chacune doit à l’ensemble d’exister, et son existence implique l’existence des autres, ce qui interdit à l’univers hadronique toute évolution, les relations entre particules étant fixées depuis l’origine. L’image du réseau s’impose comme le suggère le mot bootstrap : lacet de bottine. Si nous retrouvons bien ici l’interdépendance des monades, il s’y ajoute une idée de « self-inclusion » absente de la monadologie de Leibniz : toute monade réfléchit toutes les autres monades, qui la réfléchissent en retour ; ainsi, par ce jeu complexe de miroirs, chacune doit se réfléchir, se contenir d’une certaine manière elle-même. Cet aspect « paradoxal » de la monade se rattache au schéma général de la représentation du Tout par la partie[132] (voir annexe III) .
La monade comme palimpseste
« Nous ne percevons pas le monde, nous tirons tout de notre propre fond, tabula gravée dès l’origine, exhaustive par le savoir…,mais illisible à livre ouvert parce que les caractères en sont recouverts, effacés, défigurés…Notre entendement est, à la vérité, un palimpseste[133]« .
Cette formule de M. Serres, ainsi qu’il le fait lui-même remarquer par ailleurs, nous invite à rechercher quelque analogie monadique dans le domaine de la génétique contemporaine. Là aussi le gène, cette entité difficile à cerner, porte un message inscrit en langue primitive comme une Caractéristique Universelle que nous ne saurions pas déchiffrer, qui résume,à notre insu, ce que nous sommes et ce que nous avons en commun au sein de la multiplicité humaine. Cependant, l’analogie ne semble pleinement justifiée que pour une tendance très particulière de la génétique moderne, qui retrouve, et outrepasse même, le modèle monadique.
Dévoiements de la monade.
Par ce titre nous voulons indiquer que nous sommes conscients de quitter la piste des analogies immédiates que nous avons suivie jusqu’ici, mais aussi que le modèle monadique comporte en lui une possibilité de dérive assez dangereuse, dont nous voudrions faire état.
Il semble en effet que la frontière soit aisée à franchir entre une explication globalisante, à l’aide d’un élément fondamental unique qui traduit l’intuition d’une profonde unité de l’univers, et une forme de réductionnisme assez stérile, qui vise en dernière analyse à dénier à l’homme tout ou partie de son libre arbitre.
C’est déjà à cet écueil qu’achoppait le modèle leibnizien, et Voltaire n’a pas manqué d’ironiser sur cette insistance assez lourdaude à nous faire résigner à notre propre bonheur, arrangé pour nous par des substances qui nous dépassent. Mais si Dieu, auteur de la scénographie monadique, ingénieur d’un monde optimal, restait chez Leibniz le garant de la subordination des monades, il semble que nous assistions désormais à une émancipation de leur part, qui ne laisse pas d’être assez ridicule.
Ainsi, pour une certaine « sociobiologie », le gène serait la seule réalité fondamentale :
« Au sens darwinien,l’organisme ne vit pas pour lui-même. Sa fonction première n’est pas de reproduire d’autres organismes, il reproduit des gènes et leur sert de support temporaire[134] ».
Ces gènes, dont le caractère « éternel » semble surestimé par rapport aux possibilités de mutation, se livrent à travers nous à une guerre féroce : ils sont « altruistes », « égoïstes » ou « malveillants », ces sentiments, à notre échelle, n’étant que des illusions délibérément entretenues par eux. De la même façon que pour Leibniz le mouvement restait incompréhensible sans l’hypothèse monadique, le comportement humain sans entités sous-jacentes est pour le sociobiologiste une énigme.
De même, pour J.E. Charon, « l’homme.est un organisme qui a été inventé par les éons pour accroître le niveau de conscience des éons eux-même[135]« . Ce sont eux qui à travers les quatre interactions fondamentales, la Réflexion, la Connaissance, 1’Amour et l’Acte (dont les interprétations en termes de matrices de spin nous sont fournies dans le détail) animent le grand orchestre de l’Univers. Si désobligeant que soit pour nous cet anthropocentrisme d’un nouveau genre, il a pour contrepartie de nous assurer une pérennité rassurante : « Mort, voici ta défaite » s’écrie Charon, puisque nos éons nous survivent et nous perpétuent, transportant aux confins de 1’univers le souvenir de cet assemblage éphémère que nous fumes.
Nous sommes proches ici des conceptions de Schopenhauer sur l’amour et sur la mort, considérés comme des illusions, tandis que c’est le bon plaisir de l’espèce, de l' »archée », seule réalité stable au travers des individus fugitifs, qui s’exprime par nos transes [136]. A l’opposé, l’Egoïsme Absolu de son contemporain Stirner, cet autocratisme du Moi[137] (25) conduit à la même dénonciation comme illusion simplette de nos sentiments : c’est toujours, en définitive, pour son Moi que l’on se sacrifie, de son Moi que l’on est amoureux.
Nous voici parvenus très loin de notre point de départ. La pure monade métaphysique s’est peu à peu muée en une entité agressive, jalouse, que nous ne reconnaissons pas. Que nous en soyons composés, ou que nous la composions, ou que nous la recélions en nous à la manière d’un corps étranger, elle a pour effet de nous déposséder d’une partie de notre liberté, de jeter sur nos actes une présomption d’illusion, de nous interdire en tout cas une connaissance totale puisque nous nous heurtons à son langage caché, à cette Caractéristique que nous brûlons de saisir afin d’apprendre la vérité sur nous-même.
Noyau dur enkysté à l’intérieur de l’être, la monade relève d’une philosophie de l’invariance et d’une poétique de l’extranéité. Puissent ces charmes conjugués ne pas nous faire oublier que nous sommes nous aussi, nous avant tout, la première monade.
![]()
Annexe II : La dualité en mathématiques.
Le terme de dualité, de concept dual, apparaît dans de nombreuses branches des mathématiques. Nous en présentons ici rapidement quelques exemples. Dans le cadre de cette étude, il ne nous a pas été possible de déterminer si cette dualité se réduit, de manière plus ou moins détournée, à une notion mathématique unique. Des analogies apparaissent entre ces diverses formes de la dualité, qui militent en faveur d’une telle réduction. Et la dualité au sens des treillis et au sens de la théorie des catégories, que nous examinons en fin de chapitre, sont des notions suffisamment larges et puissantes pour englober un grand nombre de phénomènes.
A.Lautman, dans son article sur la « Symétrie et dissymétrie en mathématiques et en physique », définit la dualité comme :
- Le dédoublement d’un être complet en deux parties distinctes de l’une de l’autre par l’inversion de leur orientation.
- L’existence d’une relation involutive entre un objet O et un objet O* tel que O soit à O* ce que O*est à O, soit O = (O*)*
Dans un certain nombre de cas, seul le second aspect apparaît clairement :
Polygone dual
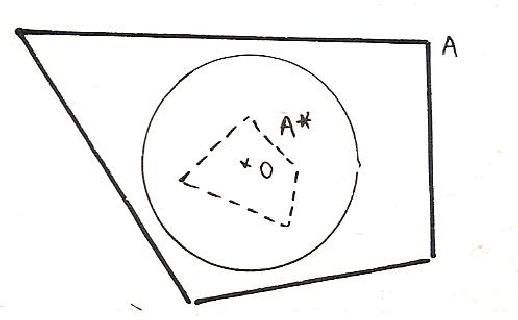 la transformation géométrique « par polaire réciproque » permet d’associer à une partie A d’un espace vectoriel une
la transformation géométrique « par polaire réciproque » permet d’associer à une partie A d’un espace vectoriel une 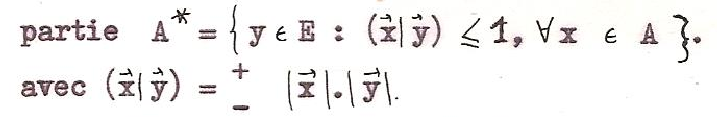
On définit ainsi une dualité pour les 5 polyèdres réguliers : si n est le nombre de côtés d’une face et m le nombre d’arêtes ayant un sommet commun,le polyèdre dual de (m, n) est (n,m). Le centre des faces de l’un devient alors les sommets de l’autre.
Matroïde dual
Nous empruntons ces exemples à C.P.Bruter (1973). La représentation duale du tétraèdre, le plus simple des matroïdes de l’espace, est :
dans le plan, on a par exemple :
Dualité en topologie
Elle transforme par exemple la boule en fuseau :
 Pour C.P. Bruter, une interprétation symbolique est possible : « ainsi l’objet est double : boule et fuseau. Le fuseau mâle, actif, créateur par l’information qu’il transporte, assure la régulation et la pérennité de la boule qui, femme, recèle le centre mystérieux et organisateur de la vie[138]«
Pour C.P. Bruter, une interprétation symbolique est possible : « ainsi l’objet est double : boule et fuseau. Le fuseau mâle, actif, créateur par l’information qu’il transporte, assure la régulation et la pérennité de la boule qui, femme, recèle le centre mystérieux et organisateur de la vie[138]«
Réseau dual
Le réseau dual, utilisé notamment en physique du solide, est tel que ses vecteurs sont reliés à ceux du réseau direct par la transformation de Fourier.
 Nous ne préciserons pas les conditions que doit respecter a pour que (a*)* = a, qui sont assez restrictives et font de cette « dualité » un cas très particulier. Nous voudrions insister sur son application en physique quantique. Pour un corpuscule isolé, la fonction d’onde s’écrit :
Nous ne préciserons pas les conditions que doit respecter a pour que (a*)* = a, qui sont assez restrictives et font de cette « dualité » un cas très particulier. Nous voudrions insister sur son application en physique quantique. Pour un corpuscule isolé, la fonction d’onde s’écrit :
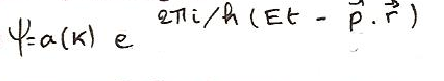 où p est l’impulsion du corpuscule. La « dualité onde-corpuscule » s’exprime justement par le fait que, dans cette formule, le vecteur 2Π/h p joue le rôle exact du vecteur d’onde k dans l’expression d’une onde plane. Une démonstration de l’inégalité de Heisenberg découle directement des propriétés de l’intégrale de Fourier : on calcule en effet, pour un train d’onde, la fonction :
où p est l’impulsion du corpuscule. La « dualité onde-corpuscule » s’exprime justement par le fait que, dans cette formule, le vecteur 2Π/h p joue le rôle exact du vecteur d’onde k dans l’expression d’une onde plane. Une démonstration de l’inégalité de Heisenberg découle directement des propriétés de l’intégrale de Fourier : on calcule en effet, pour un train d’onde, la fonction :
 qui apparaît donc comme la transformée de Fourier de a(p). On démontre alors que :
qui apparaît donc comme la transformée de Fourier de a(p). On démontre alors que :
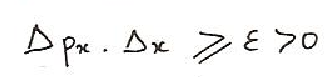 Ainsi donc, alors que pour la mécanique classique les coordonnées d’espace x et l’impulsion p étaient des variables indépendantes, elles apparaissent en mécanique quantique comme les deux variables d’une transformation de Fourier, et comme telles liées par une relation de type Heisenberg. Dès lors une seule de ces variables suffira à décrire le réel, qui apparaît donc « dual », c’est-à-dire susceptible de deux descriptions équivalentes.
Ainsi donc, alors que pour la mécanique classique les coordonnées d’espace x et l’impulsion p étaient des variables indépendantes, elles apparaissent en mécanique quantique comme les deux variables d’une transformation de Fourier, et comme telles liées par une relation de type Heisenberg. Dès lors une seule de ces variables suffira à décrire le réel, qui apparaît donc « dual », c’est-à-dire susceptible de deux descriptions équivalentes.
Dualité en logique bivalente.
Le principe de dualité établit que si A est une assertion vraie du calcul des propositions, -comprenant les opérations « et » et « ou »,l’assertion obtenue en intervertissant ces opérations est aussi une assertion vraie. Cette transformation revient à changer chaque variable logique p en sa négation p ; on comprend que, les valeurs 0 ou 1 étant purement conventionnelles, leur interversion ne doit pas modifier la validité des lois logiques. Tout se passe donc comme si la logique bivalente résultait de la fusion de deux structures parallèles, l’une en « et » et l’autre en « ou », le point de jonction étant l’opération de complémentation (négation). Comme cette opération aboutit à « changer le sens » de l’implication: (p ⇒ q) → (q ⇒ p), on peut y voir une analogie avec une symétrie. Cette dualité a des conséquences complexes: toute fonction logique peut en effet être réduite soit sous forme de polynome en « et » (^) : (…v…)^(… )^(…), soit de polynôme en « ou » (v). Certaines expressions sont « autoduales », par exemple (p v q)^(p v r)^(q v r). Mais dans le cas général, la forme minimale en « et » ne coïncide pas avec la duale de la forme minimale en « ou ». On peut interpréter graphiquement ceci, en associant à l’opération « et » la notion de :
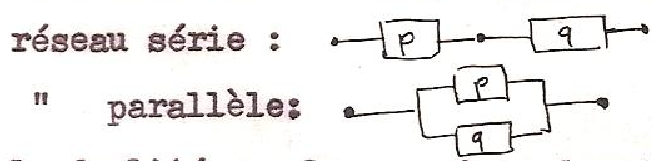 La dualité sur les polynômes revient alors à la dualité sur les graphes planaires, chaque « triangle » étant transformé en une « étoile » : on voit que cette dualité est complexe, puisqu’elle ne conserve pas le nombre de points du graphe.
La dualité sur les polynômes revient alors à la dualité sur les graphes planaires, chaque « triangle » étant transformé en une « étoile » : on voit que cette dualité est complexe, puisqu’elle ne conserve pas le nombre de points du graphe.
 Il n’y a pas de méthode générale, sinon cette interprétation graphique, pour passer de la forme minimale en « ou » à celle en « et ». Il va de soi que le dual du dual d’un réseau est ce réseau lui-même
Il n’y a pas de méthode générale, sinon cette interprétation graphique, pour passer de la forme minimale en « ou » à celle en « et ». Il va de soi que le dual du dual d’un réseau est ce réseau lui-même
Dualité dans les treillis
Un treillis est un ensemble muni de deux opérations ^ et v, chacune associative et commutative, et telles que a ^ (a v b) = a et a v (a ^ b) = a .
On voit que ces axiomes sont symétriques en ^ et v. Tout treillis est un ensemble ordonné (partiellement) par la relation a≤b <=> a ^ b = a . Ainsi a ^ b apparaît comme le Min de a et b, et a v b comme le Max. On obtient le « treillis dual » d’un treillis donné par « inversion » de l’ordre. En tant que treillis de Boole, c’est-à-dire distributif et complémenté, la dualité en logique bivalente classique se ramène à la dualité dans les treillis.
Dualité en géométrie projective.
L’espace projectif associé à un espace vectoriel E est l’ensemble P(E) des droites vectorielles de E 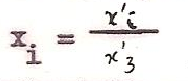 ; en dimension trois, l’espace décrit par l’espace projectif est de dimension deux : c’est donc un plan P. Les coordonnées homogènes d’un point M de P sont les coordonnées de tout point M’ situé sur la droite OM:
; en dimension trois, l’espace décrit par l’espace projectif est de dimension deux : c’est donc un plan P. Les coordonnées homogènes d’un point M de P sont les coordonnées de tout point M’ situé sur la droite OM:
Considérons la formule : 
D . Si nous considérons les ui comme fixés, nous avons l’équation d’un plan vectoriel coupant P .Ils représentent donc une droite D de P, les coordonnées homogènes de cette droite étant les xi . Si par contre, nous fixons les xi comme coordonnées homogènes d’un point de P, la formule représente toutes les droites de P passant par ce point. L’espace P peut donc être décrit en géométrie projective soit comme un ensemble de points, soit comme un ensemble de droites, et tout énoncé vrai de la géométrie projective est encore vrai en intervertissant les mots de « droite » et de « point ». Plus généralement, en dimension n pour l’espace projeté, la dualité intéresse les points et les hyperplans (dim n-1 ). Cette propriété découle directement du fait que les variétés linéaires projectives d’un espace projectif forment un treillis. Cependant, cette dualité est également liée à la dualité au sens des formes linéaires, dans la mesure où l’ensemble des hyperplans d’un espace E s’identifie à l’espace projectif P(E) de son dual.
Dualité au sens des formes linéaires.
Soit E un espace vectoriel sur le corps K.Le dual de E, E*, est l’ensemble des formes linéaires de E vers K. C’est aussi un espace vectoriel sur K, de même dimension que E dans le cas où elle est finie. On peut ensuite de la même manière définir in bidual E** En dimension trois, soit f la forme :
 Du fait de la double linéarité en xi, et en ui , on va pouvoir interpréter cette expression de deux manières :
Du fait de la double linéarité en xi, et en ui , on va pouvoir interpréter cette expression de deux manières :
 Cette duplicité de l’expression provient bien sûr de la linéarité, et du fait que tous ces espaces vectoriels sont sur le même corps K. Si l est une application linéaire entre deux espaces vectoriels E et F sur K, on peut définir l’application transposée de l, tl, par le schéma suivant :
Cette duplicité de l’expression provient bien sûr de la linéarité, et du fait que tous ces espaces vectoriels sont sur le même corps K. Si l est une application linéaire entre deux espaces vectoriels E et F sur K, on peut définir l’application transposée de l, tl, par le schéma suivant :
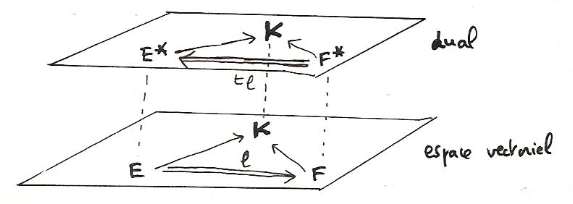 On voit que là encore il y a lors du passage de E à son dual une « inversion » du sens des flèches. Il s’agit ici d’un type très particulier de réflexion en dimension infinie, on a un morphisme injectif de E dans E** : le bidual n’est donc pas égal au dual, mais plus « large ». C’est seulement en dimension finie que le reflet du reflet s’identifie à l’original. Quant aux relations entre l’original et le monde reflété, on a un isomorphisme non canonique (donc dépendant de la base duale choisie) : c’est donc seulement dans le cas le plus simple (base duale, dimension finie) que des symétries intéressantes s’introduisent, du type :
On voit que là encore il y a lors du passage de E à son dual une « inversion » du sens des flèches. Il s’agit ici d’un type très particulier de réflexion en dimension infinie, on a un morphisme injectif de E dans E** : le bidual n’est donc pas égal au dual, mais plus « large ». C’est seulement en dimension finie que le reflet du reflet s’identifie à l’original. Quant aux relations entre l’original et le monde reflété, on a un isomorphisme non canonique (donc dépendant de la base duale choisie) : c’est donc seulement dans le cas le plus simple (base duale, dimension finie) que des symétries intéressantes s’introduisent, du type :
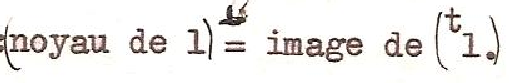
 Le grand intérêt de ces notions est qu’il s’agit sans doute de l’unique cas (lorsque toutes les conditions de simplicité sont remplies) où la connaissance d’un ensemble E s’identifie à la connaissance des fonctions appliquées à E. Cette analogie de structure entre l’argument et la fonction – entre ce qui dépend de nous et ce qui ne dépend pas de nous – découle à la fois de la linéarité, qui permet la double lecture d’une expression comme , et de la référence à un corps K unique qui sert en quelque sorte de charnière permettant de rabattre l’un sur l’autre (cf. schéma), deux mondes qu’il est habituellement interdit de confondre (voir Annexe III : La méthode de la diagonale et la construction de cercles vicieux).
Le grand intérêt de ces notions est qu’il s’agit sans doute de l’unique cas (lorsque toutes les conditions de simplicité sont remplies) où la connaissance d’un ensemble E s’identifie à la connaissance des fonctions appliquées à E. Cette analogie de structure entre l’argument et la fonction – entre ce qui dépend de nous et ce qui ne dépend pas de nous – découle à la fois de la linéarité, qui permet la double lecture d’une expression comme , et de la référence à un corps K unique qui sert en quelque sorte de charnière permettant de rabattre l’un sur l’autre (cf. schéma), deux mondes qu’il est habituellement interdit de confondre (voir Annexe III : La méthode de la diagonale et la construction de cercles vicieux).
Dualité dans la théorie des catégories.
 Le principe de dualité (métamathématique) énonce que le dual de tout théorème démontrable sur les catégories est également démontrable.
Le principe de dualité (métamathématique) énonce que le dual de tout théorème démontrable sur les catégories est également démontrable.
Le formalisme des catégories fait apparaître des symétries entre concepts mathématiques : ainsi les notions d’épimorphisme et de monomorphisme, duales pour les catégories, expliquent la symétrie des propriétés des injections et des surjections, dans le cas où les objets sont tout simplement les ensembles.
On peut as  socier une catégorie à un ensembles préordonné E, en prenant pour objets les éléments de E, et
socier une catégorie à un ensembles préordonné E, en prenant pour objets les éléments de E, et
Alors les notions de produit et de coproduit, duales pour les catégories, s’identifient dans ce cas à inf(x,y) et sup(x,y). Dans ce cas, la catégorie duale correspond à l’ensemble E avec inversion de la relation d’ordre. Nous ne savons pas si la dualité pour les treillis peut être déduite de même de la dualité catégorielle, mais cela semble vraisemblable.
On peut de même associer une catégorie à tous les espaces vectoriels Vk sur K, dont les morphismes sont les applications linéaires de ces espaces vectoriels. On peut alors définir un « foncteur dual »
qui à un espace V associe son dual (au sens des formes linéaires) et à l’application linéaire l associe sa transposée. La dualité au sens des formes linéaires peut donc être déduite de la dualité catégorielle.
Conclusion sur la dualité
En résumé, la dualité en mathématiques traduit d’abord une certaine symétrie entre propriétés, dans une formule ; cette symétrie conduit à distinguer deux objets qui se correspondent par une transformation. Lorsque cette transformation est involutive, il y a toutes chances pour qu’on puisse se ramener à la dualité des treillis, et au delà, à celle des catégories,mais en perdant ce qui fait la spécificité de l’objet.
![]()
Annexe III : La méthode de la diagonale et la construction de cercles vicieux
Les deux grandes catégories de cercles vicieux dont nous avons donné des exemples par ailleurs se retrouvent en mathématiques et en métamathématiques : le diallèle épistémologique, qui consiste à inclure dans l’hypothèse la conclusion d’un raisonnement, est l’ennemi de toute axiomatisation. Des exemples célèbres et controversés de tels cercles se trouveraient facilement, dans l’histoire notamment de la théorie des ensembles : définition du nombre par Russell (selon Hilbert), axiome de choix et bon ordre chez Zermelo (selon Borel)… Nous nous intéresserons ici exclusivement au second type de diallèle, lié au pouvoir de thématisation de l’esprit, à travers les exemples des paradoxes de Russell et du théorème d’incomplétude de Gödel. Il ne s’agira pas bien sûr de restituer tout l’appareil mathématique et logique dont ils découlent ou qu’ils ont suscité ; nous voudrions simplement montrer comment la construction effective d’un cercle vicieux – importune dans le premier cas, délibérée dans le deuxième – découle d’un même mouvement de l’esprit, matérialisé par le raisonnement dit « de la diagonale ».
Si,par leur rigueur formelle, ces constructions contribuent à clarifier les origines et le mécanisme du diallèle, elles n’en restent pas moins redevables aux approches antérieures, dont elles reprennent le panorama intuitif. Nous verrons que le « vice », la difficulté à en dominer pleinement les tenants et aboutissants, provient justement de l’imbrication des intuitions primitives à l’intérieur de cette figure complexe. Avant de commencer directement son analyse, il convient donc de présenter séparément quelques thèmes qui lui sont intimement liés.
Thématique du cercle vicieux.
Dualité
Platon, dans un-passage du Parménide, remarque que s’il y a un nombre tel que 1, alors 1 a une existence. Mais 1 est différent de l’Etre. Un et l’Etre sont deux, deux et l’Etre sont trois, et ainsi de suite. Russell, qui cite ce passage[139], s’interroge sur sa validité. En effet, à supposer qu’il n’y ait aucun objet dans le monde, la considération de l’ensemble {Ø} (ensemble dont le seul élément est l’ensemble vide), puis de l’ensemble {Ø,{Ø}} et ainsi de suite, permet de construire un ensemble de cardinal aussi grand que l’on désire (donc rend inutile l’introduction d’un axiome de l’infini). Il s’agit là, selon lui, d’une illusion due à la confusion des types, l’ensemble et l’élément – ou l’Etre et le nombre chez Platon – ne pouvant être réunis impunément en une entité synthétique.
Cependant, Von Neumann et Bernays ont construit les nombres ordinaux finis selon ce procédé, définissant pour tout ensemble x un « successeur » x+ = x U {x}, et identifiant 0 à l’ensemble vide, le nombre 1 au successeur de 0, etc…. (l’axiome d’infinité devient, dans cette optique : il existe un ensemble A contenant 0 et contenant le successeur de chacun des éléments de A).
Ces considérations n’ont d’autre but que de présenter le domaine de prédilection du diallèle : il se situera toujours à cheval entre deux Mondes, 1’un plus « abstrait » que l’autre, résultant de l’intervention d’un Deus ex machina immanent : le passage de х à {x},du nombre à la constatation de son existence, révèle l’irréductible intrusion d’une entité classante, ou observante.
Formation d’un mixte autonome
Ayant donc constaté la dualité des domaines de l’être et de l’idée, l’esprit s’inquiète de trouver un terme charnière, participant de l’un et de l’autre. La preuve ontologique est l’exemple-type de cette exigence : il s’agit de définir Dieu comme une entité autonome, à la fois vis à vis des contingences du monde réel et de l’arbitraire des concepts, une entité « close » sur elle-même, « enveloppant » dans son essence la nécessité de son existence. Dans le paradoxe de l’Epimenide, à l’inverse, on forme un énoncé renfermant en lui-même la preuve de sa propre fausseté. Cependant, les deux démarches ont le commun souci d’établir une liaison forcée entre deux mondes auparavant indépendants, par l’intermédiaire d’une entité maximale : Dieu, qui est le « plus grand » ou le « plus parfait », ou le menteur, qui ment toujours.
 Analysons, en le développant beaucoup, le fonctionnement de la preuve dite de Saint Anselme.
Analysons, en le développant beaucoup, le fonctionnement de la preuve dite de Saint Anselme.
Dans le monde des idées, il y a deux domaines:
- D1, ensemble des idées correspondant à un être réel ;
- D2, ensemble des idées purement fictives (le triangle rond).
Définissons une « chose maximale » (C.M.) par « chose telle que l’on n’en puisse concevoir de plus grande. » Il nous faut démontrer que de la seule définition de l’idée (C.M.) découle son existence ; en d’autres termes, que (C.M.) appartient à D1 .
A priori, une telle chose maximale (C.M.) peut exister (C.M.)1 ou ne pas exister (C.M.)2 . Cependant, nous « pouvons concevoir » une (C.M.)1 qui possède la propriété d’exister, et appartient donc à D1 (même si nous ne savons rien sur la validité de cette assertion). Nous avons donc l’idée d’une idée (C.M.)1 « plus grande » que (C.M.)2 , puisque (C.M.)1 = (C.M.)2 + existence, ce qui signifie que (C.M.)2 n’est pas une chose maximale, ce qui contredit sa définition. Donc il n’y a pas de chose maximale dans D2. Donc elle est dans D1. Donc elle a un correspondant réel.
Ce raisonnement est exemplaire tant par les diverses difficultés qu’il brasse inextricablement que par les critiques qu’il a encourues : le point faible est évidemment une « confusion des types » platonicienne dans la considération de l’existence comme un terme additionnable. La correction par Descartes du « plus grand » en « plus parfait » vise à rendre moins brutale cette assimilation. Mais Gassendi ne s’y trompe pas : l’existence n’est pas une perfection, c’est une forme ou un acte, quelque chose d’un niveau supérieur à celui des simples propriétés de l’objet. Kant mêmement dénonce cette confusion :« cent thalers réels ne contiennent rien de plus que cent thalers dans l’esprit » car sinon, la pensée ne serait plus « adéquate » à l’être.
Cependant, au niveau non formalisé où nous nous plaçons, cette querelle syntaxique n’apparaît pas déterminante. Pourquoi ne pourrait-on définir un langage où l' »existence » signifierait, sous une quelconque forme, un « accroissement » de l’objet?
Le moment crucial du raisonnement réside plutôt dans le « pouvoir concevoir » de la définition, expression remarquablement ambigüe. Car si en effet nous « pouvons concevoir » une (C.M.) appartenant à D1 , nous pouvons aussi concevoir, en vertu de la même liberté de thématisation, une (C.M.) appartenant à D2. Or le raisonnement, considérant seulement la première possibilité, démontre l' »absurdité » de la seconde que nous « pouvons concevoir » pourtant au même titre que la première. Le « pouvoir » est donc entendu en deux sens : l’un, explicite, désigne la capacité illimitée de l’esprit à former des concepts, sans se préoccuper de leur validité (le triangle rond) ; l’autre exige du concept créé une cohérence logique, par rapport à un système syntaxique non défini explicitement.
Cette absence d’une référence normative stable ôte au raisonnement toute pertinence. Comme le remarque très justement Leibniz, il prouve seulement que si la notion de « chose parfaite » n’est pas contradictoire et si on admet que l’existence est une perfection, alors la chose parfaite existe. Quant à la première condition, la seule importante, elle est occultée dans la démonstration de St Anselme par une fausse dichotomie, puisqu’on ne définit pas le domaine D3 des concepts « absurdes ».
La preuve ontologique nous offre, à l’état brut, un résumé des difficultés que nous allons rencontrer constamment, ce qui justifie ce développement un peu long :
- définition d’une « chose maximale » comme dans le 1° paradoxe de Russell,
- confusion des types comme dans le 2°,
- nécessité d’un système de référence garantissant la validité des propositions, comme dans le théorème de Gödel.
Il apparaît déjà que la résolution des paradoxes passera sans doute par la limitation du pouvoir de thématisation de l’esprit.
Réflexion et emboîtement
Un dernier thème intimement lié à la nature du cercle vicieux est celui de la réflectivité. En effet, le deuxième monde (ensembles, propositions, idées) nous donne une représentation du premier (éléments, faits, objets réels). Dès lors que nous construisons un mixte homogène à ces deux mondes, cette entité distinguée devient en quelque sorte la représentation d’elle-même. Ce problème de l' »autoréference », très difficile à cerner, semble à lui seul paradoxal.
Royce fait remarquer qu’une carte visant à tout représenter devrait se contenir elle-même à une échelle réduite, et ainsi de suite à l’infini : même régression vertigineuse qu’entre deux miroirs face à face.
De même, Cantor affirme se figurer un ensemble « comme un abîme » : l’ensemble des nombres pairs ne constitue-t-il pas une sorte de réflexion interne, une carte des nombres naturels, puis l’ensemble des multiples de quatre, de six, etc [140]?
C’est Dedekind qui poussera le plus loin l’axiomatisation de cette construction « en abîme » en introduisant le concept de « chaîne » : Φ étant une application interne d’un ensemble, une partie M telle que Φ(M) reste incluse dans M est une chaîne, cette inclusion conditionnant un emboîtement descendant. Le caractère de chaîne permet de retrouver les principaux résultats de la théorie des nombres cardinaux, et fournit notamment une caractérisation originale d’un système infini S comme devant être semblable (i.e. lié par une injection) à une de ses parties propres (distincte de S). La démonstration d’existence d’un tel ensemble infini se réfère directement au problème de la thématisation qui nous occupe : l’exemple exhibé est en effet
« l’ensemble S de toutes les choses qui peuvent être objet de ma pensée… Car si s désigne un élément de S, la pensée s’ que s peut être objet de ma pensée, est elle-même un élément de S. Si l’on considère le même élément s’ comme l’image Φ(s) de l’élément s, l’application de S ainsi définie a la propriété que l’image S’ est une partie propre de S… car il y a dans S des éléments (par exemple mon moi) qui sont distincts de toute pensée s’ de ce genre.[141]«
Pour conclure ce catalogue thématique, ajoutons que l’on peut considérer le diallèle, avec R. Thom[142], comme exprimant un paradoxe de l’identité :
- identité locale, liée au lieu spatial, de l’être considéré comme un objet matériel.
- identité sémantique, délocalisée, de l’être considéré comme un objet abstrait.
C’est du conflit entre ces deux critères d’identité, de la duplicité de l’objet, que naîtrait, dans le cas qui nous occupe, le cercle vicieux ; et plus généralement, l’imaginaire…
La méthode de la diagonale
La méthode de la diagonale fut introduite par Cantor en 1890[143] pour la démonstration de la non-dénombrabilité du segment réel [0, 1].
Si [0, 1] était dénombrable (pouvait être mis en correspondance biunivoque avec l’ensemble N des entiers naturels), on pourrait ordonner tous les réels, exprimés par leur développement décimal, en une suite indexée par N : x1, x2… xn. Inscrivons la liste de ces nombres, avec toutes leurs décimales :
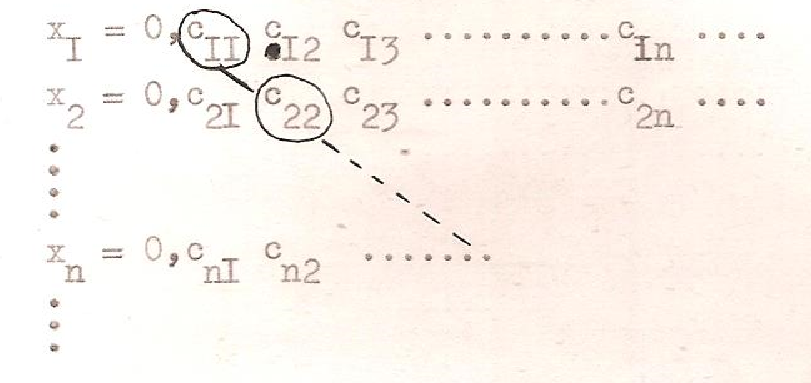
Considérant la diagonale du tableau, nous pouvons former un réel x = 0,a1a2 … an … tel que pour tout n, an soit différent de cnn (et an ≠ 0). Il est clair que ce réel x, par construction, ne peut figurer nulle part dans la suite x : l’hypothèse d’une correspondance biunivoque est donc fausse.
Nous voyons apparaître d’ores et déjà dans cet exemple très simple les moments essentiels de la méthode de la diagonale : raisonnement par l’absurde, liaison universelle supposée entre deux collections ; puis, à partir d’une totalité d’objets considérée comme donnée (ici, la suite des xn, dont on ne nous dit aucunement comment la construire), on construit, cette fois explicitement, un nouvel objet x n’appartenant pas à cette totalité [144].
Une autre démonstration de Cantor va nous permettre de voir se déployer plus complètement les caractéristiques de cette méthode.
On désire montrer qu’un ensemble quelconque E et l’ensemble de ses parties PE ne peuvent être mis en correspondance biunivoque (en d’autres termes, le cardinal – nombre d’éléments – de PE est strictement supérieur au cardinal de E, proposition évidente dans le cas d’ensembles finis, mais qu’il s’agit d’étendre aux ensembles infinis).
Supposons qu’il existe une telle bijection, qui à tout élément x de E associe une partie Px ,et réciproquement. Nous allons, à partir de cette seule hypothèse, construire une partie D qui ne sera l’image d’aucun élément d.
Première étape : construction de D. Nous allons nous aider d’un schéma, qui ne joue aucun rôle dans la démonstration, mais permet de justifier intuitivement le terme de « diagonale ».
 Convenons de représenter E par un segment, et de relier deux points x et y si x appartient à l’image de y (x ϵ Py ).
Convenons de représenter E par un segment, et de relier deux points x et y si x appartient à l’image de y (x ϵ Py ).
Il peut se faire que certains éléments soient tels qu’ils appartiennent à leur propre image (x ϵ Px ) Leurs points représentatifs figureront sur la diagonale. Les points manquants sur la diagonale définiront donc 1’ensemble D des points n’appartenant pas à leur image :
Deuxième étape : D étant une partie de E, on doit par la bijection définie sur toutes les parties lui faire correspondre un élément d tel que D = Pd. Demandons nous alors si d appartient à Pd . On obtient alors le cercle vicieux suivant, qu’on peut lire dans les deux sens :
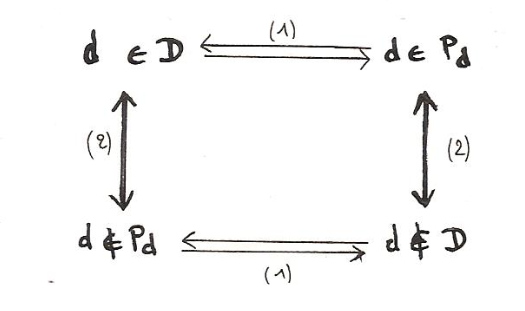 Ainsi, on doit conclure que d ne peut être trouvé, puisqu’il conduit à une absurdité. Il n’y a donc pas de bijection entre E et PE ce qui termine la démonstration.
Ainsi, on doit conclure que d ne peut être trouvé, puisqu’il conduit à une absurdité. Il n’y a donc pas de bijection entre E et PE ce qui termine la démonstration.
Mais il nous faut étudier de plus près la nature de ce cercle : nous venons de construire une proposition indécidable « d appartient à D » dont la valeur de vérité oscille lorsqu’on parcourt le cercle.
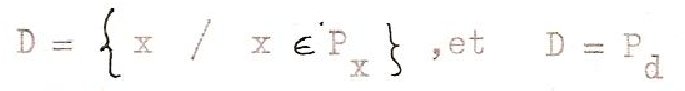 Supposons que nous ayons posé plutôt :
Supposons que nous ayons posé plutôt :
Se demander si un élément x appartient ou non à D impose de parcourir toute l’extension de l’ensemble Px, supposé accessible. Si maintenant pour x nous prenons d, se demander si d appartient à D revient à parcourir l’extension de Pd ,c’est à dire de D, afin de déterminer si d appartient à D. Dans ce cas également, nous obtenons donc un cercle « épistémologique », moins « vicieux » peut-être que le précédent, puisqu’il n’introduit pas de contradiction, mais qui interdit néanmoins de conclure faute de point de départ :
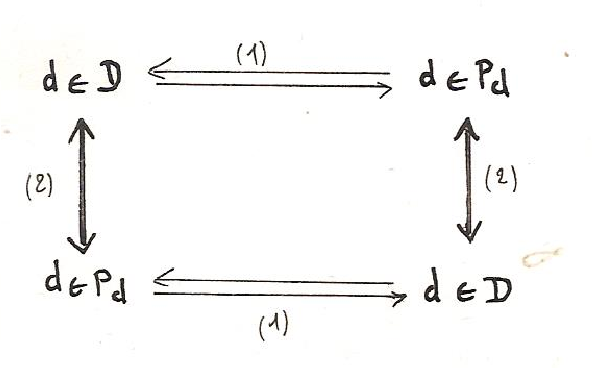 Dans l’un ou l’autre de ces cercles, deux types d’implication apparaissent :
Dans l’un ou l’autre de ces cercles, deux types d’implication apparaissent :
- l’implication (1) est liée à une définition « externe » de D, comme élément de l’ensemble des parties PE : D = {…}
- l’implication (2) tient à une définition « interne » de D : tous les x tels que
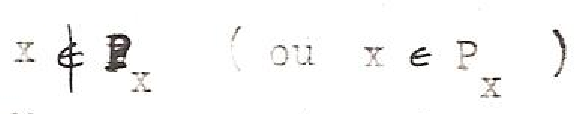
Nous pressentons donc que la circularité tient à une double nature de D, qu’il convient de préciser.
Qu’en est-il de l’ensemble PE ? Nous savons qu’il existe, car nous avons en tête des procédés pour le construire, tout au moins dans le cas d’ensembles finis. Cependant, la définition externe (1) de D n’utilise en rien cette constructivité : il suffit que nous reconnaissions D comme un élément de PE (c’est à dire comme une image par bijection), sans pour autant énumérer les autres éléments de PE. En d’autres termes, PE apparaît ici comme une totalité actuelle, sans que nous en connaissions explicitement le contenu.
Par contre, la définition interne (2) impose que nous parcourions effectivement toutes les parties Px de PE , afin de déterminer si x appartient ou non à Px . PE est donc visé ici à titre de totalité potentielle.
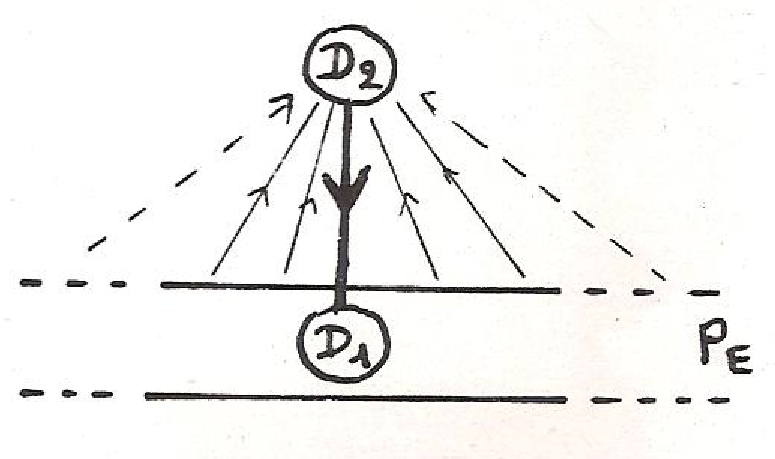 En d’autres termes :
En d’autres termes :
- la définition (1) pose D1 comme élément d’une totalité non définie, dans laquelle il est immergé.
- la définition (2) présente D2, au contraire, comme un objet « surplombant », dont l’existence est seconde par rapport à celle du substrat PE.
- D1 = partie de PE
- D2 = objet dont l’existence découle de la considération de toutes les parties de PE
Le cercle vicieux s’établit dès lors que nous forçons l’objet D2 à s’incarner en un objet D1 (i.e. nous lui supposons un antécédent bijectif). Car, étant défini en dépendance de toutes les parties, il devient défini en quelque sorte à partir de lui-même ; nous reviendrons plus loin sur cette question de la non-prédicativité.
Avant de quitter cette démonstration, où nous avons vu jouer les mécanismes essentiels de la méthode de la diagonale, remarquons que sa conclusion « d n’existe pas puisque son existence conduit à un cercle vicieux » est discutable. Ne peut-on imputer l’origine de cette contradiction au présupposé d’une bijection dont on ne sait rien, sur l’ensemble non explicitement déterminé PE ? C’est ce caractère d’actualité (ce « moment extra-syntaxique » selon l’expression de J. Toussaint-Desanti) qui, pour les mathématiciens intuitionnistes, invalide toute démonstration basée sur la méthode de la diagonale.
Les paradoxes de Russell
Il n’est pas dans notre propos de rappeler le déroulement de la « crise des fondements » en mathématiques, ni le rôle que les « antinomies » ont joué dans l’abandon de la théorie naïve des ensembles. Nous voudrions simplement présenter le schéma de deux paradoxes célèbres, généralement attribués à Russell, et qui découlent directement de la méthode cantorienne de la diagonale.
« L’ensemble de tous les ensembles »
La démonstration précédente prouve que l’inégalité stricte du nombre des éléments et du nombre des parties d’un ensemble peut être étendue aux ensembles infinis.
Or l’ensemble de tous les ensembles, s’il existe, contient toutes ses parties (qui sont des ensembles) à titre d’éléments : il ne peut donc avoir plus de parties que d’éléments, contrairement à l’inégalité précédente. (2n > n).
Nous ne nous attarderons pas sur ce paradoxe, qui repose sur le cercle déjà étudié. Montrons simplement comment le troisième axiome de Zermelo, dit axiome de sélection (Aussonderung) permet d’éliminer la contradiction. Selon cet axiome :
« si une proposition S(x) est « définie » pour tous les éléments d’un ensemble A, A possède toujours une partie B constituée par tous les éléments x de A pour lesquels S(x) est vraie[145] ».
Autrement dit, seul peut être nommé ensemble un système d’objets qui sont par ailleurs éléments d’un ensemble A déjà reconnu comme tel. Cette restriction « descendante » permet de démontrer que, pour tout ensemble A, il existe toujours un ensemble B qui n’appartient pas à A (donc impossibilité d’un ensemble de tous les ensembles)
 « L’ensemble des ensembles qui n’appartiennent pas à eux-même «
« L’ensemble des ensembles qui n’appartiennent pas à eux-même «
Exposons les différentes étapes de ce paradoxe :
- un principe « d’abstraction » postule qu’à toute fonction propositionnelle S(x), il est possible d’associer un ensemble, celui dont les éléments vérifient S.
- soit .
 . Donc, d’ap
. Donc, d’ap  rès le principe ci-dessus, il existe un ensemble D tel que, pour tout x,
rès le principe ci-dessus, il existe un ensemble D tel que, pour tout x, - or x étant libre dans cette expression, on peut prendre justement x = D. D est l’ensemble des ensembles qui n’appartiennent pas à eux-même.
Ici encore, le cercle peut être parcouru dans les deux sens.
L’équivalence (1) est purement tautologique.
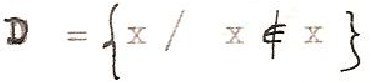 L’équivalence (2) se réfère à la définition « interne »
L’équivalence (2) se réfère à la définition « interne »
L’intérêt de ce paradoxe réside principalement dans la diversité des tentatives de résolution qu’il a inspirées. Reprenons brièvement les principales. On voit que le point crucial du paradoxe est la formation de ![]() la fonction
la fonction
- Une première idée peut être d’interpréter la négation dans une logique plus faible que la logique classique[146]. Elle ne semble pas conduire à des résultats intéressants.
- On peut chercher à limiter le principe d’abstraction, de façon à ce qu’il ne corresponde aucun ensemble à la fonction
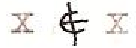 . C’est la voie classique de résolution du paradoxe, qui a prévalu jusqu’ici (Zermelo, Von Neumann…). Reprenant l’idée de l’axiome de sélection, elle conduit à distinguer classe et ensemble : une fonction propositionnelle S(x) définit toujours une classe. Par contre, B est un ensemble si et seulement si il existe une classe A telle que B ϵ A. Une classe n’a donc pour éléments que des ensembles ; tout ensemble est lui même une classe ; par contre, il existe des classes qui ne sont pas des ensembles. La classe D définie plus haut est de ce type : si D était un ensemble, alors on aurait :
. C’est la voie classique de résolution du paradoxe, qui a prévalu jusqu’ici (Zermelo, Von Neumann…). Reprenant l’idée de l’axiome de sélection, elle conduit à distinguer classe et ensemble : une fonction propositionnelle S(x) définit toujours une classe. Par contre, B est un ensemble si et seulement si il existe une classe A telle que B ϵ A. Une classe n’a donc pour éléments que des ensembles ; tout ensemble est lui même une classe ; par contre, il existe des classes qui ne sont pas des ensembles. La classe D définie plus haut est de ce type : si D était un ensemble, alors on aurait :
 Du fait de la conjonction dans le second membre, on évite la contradiction précédente : il suffit de conclure : il n’existe pas de classe A telle que D ϵ A.
Du fait de la conjonction dans le second membre, on évite la contradiction précédente : il suffit de conclure : il n’existe pas de classe A telle que D ϵ A.
- Cependant, cette solutio
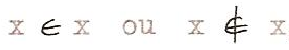 n, si elle lève le paradoxe, ne pouvait manquer de paraître très artificielle à un logicien aussi profond que Russell. Pour lui, la faute était à rechercher dans la formation de la fonction propositionnelle S(x). Il doit y avoir des expressions interdites, comme , l’élément n’étant pas « du même ordre » que l’ensemble. La formalisation de cette intuition duale conduit à la redoutable « théorie des types », exposée dans les Principia Mathematica, et que les difficultés de notation et de compréhension ont fait peu à peu tomber en déshérence. Ainsi :
n, si elle lève le paradoxe, ne pouvait manquer de paraître très artificielle à un logicien aussi profond que Russell. Pour lui, la faute était à rechercher dans la formation de la fonction propositionnelle S(x). Il doit y avoir des expressions interdites, comme , l’élément n’étant pas « du même ordre » que l’ensemble. La formalisation de cette intuition duale conduit à la redoutable « théorie des types », exposée dans les Principia Mathematica, et que les difficultés de notation et de compréhension ont fait peu à peu tomber en déshérence. Ainsi :
- les fonctions d’ordre 1 ont pour argument des individus ;
- les fonctions d’ordre 2 des propositions d’ordre 1 ;
- les fonctions d’ordre 3, des individus, des propositions d’ordre 1, ou deux propositions d’ordre 2…, chaque ordre n se subdivisant en 2n-1 types [147]. Quoi qu’il en soit, cette théorie conduit à n’appliquer le principe d’abstraction qu’à des expressions stratifiées, l’argument à gauche du signe ϵ devant être d’ordre (ou de type) inférieur à celui de l’argument de droite.
Nous avons donc ici un nouvel exemple où la rupture de la circularité passe par l’établissement d’une hiérarchie, c’est-à-dire d’une régression à l’infini.
- Remarquons que les développements de la logique combinatoire (Curry, 1958) éclairent d’un jour nouveau ce paradoxe. Dans cette logique, on peut en effet construire un combinateur paradoxal Y, qui permet de dériver toute proposition et son contraire.Pour éviter la contradiction, on définit des catégories, à l’intérieur desquelles on limite certains axiomes[148].
Pour en terminer avec ce paradoxe de Russell, nous voudrions en exposer une interprétation moins technique. Gonseth[149] utilise à cet effet l’analogie avec un « catalogue de catalogues » :
 un catalogue peut citer un ouvrage (relation A) ou ne pas le citer (relation B). En particulier, il peut se citer lui-même (cas a) ou ne pas se citer (cas b).
un catalogue peut citer un ouvrage (relation A) ou ne pas le citer (relation B). En particulier, il peut se citer lui-même (cas a) ou ne pas se citer (cas b).
Soit c le catalogue des catalogues qui ne se citent pas eux-même, c’est à dire que c a la relation A avec tous les objets qui ont avec eux-même B, et réciproquement. On en conclut que c a avec lui-même les deux relations A et B simultanément.
Or, si dans le cas général, il n’y a aucun inconvénient à imaginer un nombre quelconque de relations d’un objet envers lui-même, dans le cas qui nous occupe les relations A et B sont choisies pour être incompatibles. Gonseth en conclut qu’ « on n’est pas libre de décider arbitrairement que telles ou telles de ces relations doivent s’exclure ou s’accompagner nécessairement l’une l’autre ».
Si nous comprenons bien cet auteur, son opinion semble être que dès lors qu’un système d’objets est fixé (donc les relations entre eux), on n’est plus libre de décider arbitrairement des relations entretenues par un nouveau terme, puisque celui-ci doit forcément appartenir au système initial. Le cercle vicieux ne serait donc que la réponse désespérée du système à l’intrusion d’un terme qui n’y a pas sa place. Pour clarifier ceci, une nouvelle – et dernière- forme du paradoxe de Russell est plus adéquate : c’est le casse-tête connu du « barbier qui rase tous ceux qui ne se rasent pas eux-même ».
 Tout homme est susceptible de raser (relation R) ou d’être rasé (relation ER) Nous pouvons de répartir les hommes du village en deux classes: ceux qui se rasent, et ceux qui sont rasés par autrui, tout autre cas étant exclu.
Tout homme est susceptible de raser (relation R) ou d’être rasé (relation ER) Nous pouvons de répartir les hommes du village en deux classes: ceux qui se rasent, et ceux qui sont rasés par autrui, tout autre cas étant exclu.
Mais cette dichotomie s’avère fausse dès que nous considérons le cas intermédiaire du barbier, qui peut à la fois raser et être rasé. Le paradoxe se crée lorsque nous forçons le système binaire des villageois à s’incorporer un terme non prévu pour lequel il n’est pas structuré.
En deçà des développements techniques qu’il a inspirés, le fonctionnement du paradoxe de Russell semble bien être analogue à celui de ces exemples simplets. Dans tous les cas, on trouve une relation à la fois « passive » et « active » : être contenu/contenir ; être rasé/raser (transitive ou non-transitive d’ailleurs). Cette structure permet évidemment à la relation d’être « pronominale » : se raser
 R1 : contenir autrui
R1 : contenir autrui
R2 : être contenu par autrui
R3 : contenir et être contenu, se contenir.
On voit que les relations binaires R1 et R2 ne sont que les deux composantes d’une relation « ternaire » R3 ,liant à égalité trois objets. Il est clair que lorsque ces trois objets sont différents, aucune contradiction n’apparaît :
 O2 peut parfaitement ne pas contenir O1 et être contenu par O3 .
O2 peut parfaitement ne pas contenir O1 et être contenu par O3 .
Le paradoxe intervient lorsque les trois objets sont égaux et que nous essayons d’interpréter la relation ternaire en terme de deux relations binaires : on obtient évidemment O contient O et O ne contient pas O.
 Si donc dans la grande majorité des cas la pensée binaire suffit, on peut construire une configuration où, faute de reconstituer l’intégralité de la relation ternaire, on s’oblige à ne percevoir que deux moitiés contradictoires de la réalité. Remarquons que cette relation ternaire, quoique plus adéquate, n’est encore qu’une restriction ne permettant pas d’envisager des cas comme :
Si donc dans la grande majorité des cas la pensée binaire suffit, on peut construire une configuration où, faute de reconstituer l’intégralité de la relation ternaire, on s’oblige à ne percevoir que deux moitiés contradictoires de la réalité. Remarquons que cette relation ternaire, quoique plus adéquate, n’est encore qu’une restriction ne permettant pas d’envisager des cas comme :
Seule la considération d’une relation n-aire éliminerait tout paradoxe.
Comment ne pas penser ici au concept de holon introduit par A. Koestler, cette entité à faces de Janus tournées l’une vers la passivité, l’autre vers l’action[150] : seule la prise en compte simultanée des deux est susceptible de conduire à une perception correcte de la hiérarchie qu’elles composent.
Du paradoxe du menteur au théorème de limitation de Gödel
Les paradoxes que nous avons examinés au paragraphe précédent sont corrélatifs aux premières tentatives d’axiomatisation de la théorie des ensembles, au début du XX° siècle. A la même époque furent construites des « antinomies » mettant en jeu une dimension sémantique, qui précédaient l’émergence de la notion de système formel. Les plus connues sont celle de Berry et celle de Richard, dont le théorème de Gödel constitue l’explication et le développement logique.
Le paradoxe de Berry
Il repose sur la formation d’un énoncé du type de D : « d est le plus petit entier non définissable de manière unique par une phrase française de moins de 1000 lettres. » Or l’énoncé D lui-même définit l’entier d visiblement en moins de 1000 lettres, d’où la contradiction.
Une critique immédiate (voir par ex. Gonseth, op. cit.) porte sur le « de manière unique ». Peut-on vraiment classer les entiers par le nombre de lettres de leur définition en langage non-formalisé ? Mais, admettant même que ceci soit possible, l’objection majeure reste celle de Poincaré :
« la classification des nombres peut être fixée seulement après que la sélection des définitions soit complète, et la sélection des définitions peut être complète seulement après que la classification soit terminée, de sorte que ni la classification ni la sélection ne sont jamais terminées.[151] »
Le paradoxe provient donc de la forme même de D : D donne d’une part une définition « interne » de d, qui suppose d’avoir nettement séparé, de manière actuelle, les entiers définissables d’une certaine manière de ceux qui ne le sont pas. Or il se trouve que D, par sa forme « externe », est justement une définition d’entier d. Pour savoir si d appartient à l’une ou l’autre classe, il faut donc parcourir l’extension potentielle de E, afin d’y trouver D qui, justement n’a de sens qu’une fois achevé ce parcours. Même dualité donc entre infini actuel et infini potentiel que celle que nous avions décelée dans l’argument de la diagonale.
Ainsi, pour Poincaré, D est une proposition « imprédicative », c’est-à-dire dont la valeur de vérité est altérée par l’introduction de nouveaux éléments dans le système E qu’elle régit. En particulier, la valeur de vérité de D est altérée lorsqu’on injecte D elle-même, en vertu de sa forme externe, dans le système E. En termes leibniziens, D représente d’une certaine manière le multiple réfléchi dans l’un ; et la liaison monadique universelle qu’elle entretient avec les autres propositions « atomiques » devient paradoxale lorsqu’on s’avise qu’elle s’applique en particulier à D elle-même.
Le paradoxe de Richards
Il concerne les expressions en langue anglaise qui sont les définitions de propriétés d’entiers[152]. Elles sont donc en nombre dénombrable, et nous pouvons les ordonner en une suite P1, P2… Pn (par exemple d’abord suivant le nombre de lettres et ensuite suivant l’ordre lexicographique, dans les cas d’égalité de ce nombre.)
Pour un entier x donné, on a en général « x possède la propriété Py« , ce que nous noterons : Py(x). Définissons maintenant la propriété D : »n n’a pas la propriété Pn » , ce qui se note D(n) = non Pn(n). D étant une propriété d’entiers, il existe un rang d tel que D=Pd. Soit, pour tout n, D(n)= Pd(n) . Prenant n = d, on obtient : D(d) = Pd(d) alors que par définition : D(d) = non Pd(d).
On voit que ce raisonnement est exactement calqué sur la méthode de la diagonale, mais appliquée ici non aux objets mathématiques eux-même (les entiers), mais aux propriétés de ces objets, exprimées dans un formalisme qui se cherche (ici, la langue naturelle, l’anglais). La propriété D dépend de la manière d’ordonner toutes les propriétés des entiers, posées comme données ; c’est donc une propriété purement métamathématique.
Le progrès décisif effectué par Gödel va être de trouver le moyen d’exprimer des propriétés métamathématiques dans un langage identique au domaine-objet (1’arithmétique), ce qui élimine l’objection de Gonseth.
Ce théorème central de Godel prélude à une série d’autres résultats fondamentaux portant sur les limitations des systèmes formels (Church, Kleene, Tarski…) et clôt en même temps l’histoire complexe des interrogations sur la validité des langages naturels, que la rencontre fortuite de paradoxes avait pu susciter. Avant de l’aborder directement, il nous semble intéressant de donner un exemple de ces paradoxes naturels, afin de nous situer d’abord sur un terrain plus familier.
La paradoxe du menteur
Il s’agit du célèbre paradoxe du menteur, dit encore du Crétois ou de l’Epiménide, sur lequel nous allons nous livrer à une tentative de mise en forme certes inutile eu égard à la simplicité du paradoxe, mais qui va nous révéler sa profonde similitude – la rigueur en moins -, avec l’idée de base de la démonstration de Gödel.
Le paradoxe dénonce la proposition « D » : « je suis un menteur » comme étant indécidable. Nous voudrions montrer que cette proposition, si immédiatement claire, peut être considérée comme le résultat d’un procédé diagonal implicite.
Soit O le domaine-objet constitué par les locuteurs, et L le domaine linguistique des propositions portant sur ces objets. Soient a et b deux tels objets, à savoir des locuteurs. Nous pouvons définir Pa(b) : proposition énoncée par a sur b. Définissons l’objet m, le menteur, par :
« pour toute proposition Pm et tout argument b, Pm(b) est fausse ».
La définition du menteur, comme celle de l’ensemble E ou du prédicat D dans la méthode de la diagonale, repose à la fois sur une propriété négative et sur la considération d’un ensemble actuellement infini (ici,la richesse du langage naturel oblige à considérer une double infinité, celle des locuteurs et celle des propositions qu’ils énoncent ).
Nous pouvons maintenant fixer successivement les deux variables :
- choisir la proposition Pm(b)=m, par laquelle m dit : « b est un menteur »
- puis choisir comme argument b le locuteur m : m dit « m est un menteur », soit « je suis un menteur ».
.
Montrons que cette proposition « D1» est indécidable, en notant D1 le fait réel : je suis un menteur.
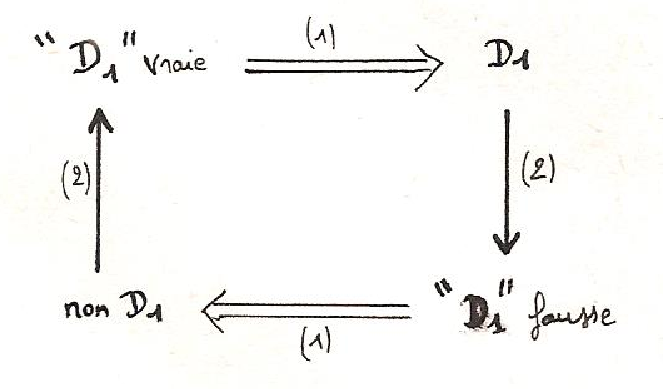 On voit que le cercle vicieux traduit une oscillation permanente entre le plan L du langage et le plan O du domaine-objet. Cependant, ainsi que nous l’avons déjà remarqué, les deux transitions sont de natures très différentes :
On voit que le cercle vicieux traduit une oscillation permanente entre le plan L du langage et le plan O du domaine-objet. Cependant, ainsi que nous l’avons déjà remarqué, les deux transitions sont de natures très différentes :
་
- l’implication (1) (L→O) traduit la « bijection canonique » qui est supposée exister afin que la représentation L de O soit valide : à un énoncé vrai doit correspondre un fait réel.
- l’implication (2) (O→L) découle de la définition de m, qui ne dépend que de la liberté de former des énoncés consentie au système linguistique.
Il nous est possible de préciser maintenant ce que nous entendions par dualité interne / externe :
- interne signifie « à l’intérieur d’un système de représentation », ici le langage L, ailleurs l’ensemble des parties PE (on peut en effet comprendre PE comme l’ensemble des prédicats s’appliquant aux objets de E[153] ).
- externe signifie « en tant qu’objet, sans signification sémantique ».
Il est clair que si ces deux points de vue peuvent coexister en « D1», c’est du fait de sa nature de proposition de proposition qui résulte de la construction diagonale : la liberté de thématisation permet à D1/« D1» de revendiquer l’appartenance alternativement aux domaines O et L.
La particularité de ce cercle par rapport à ceux précédemment obtenus, est qu’il ne peut visiblement être parcouru que dans un seul sens, puisqu’il n’utilise la bijection canonique que dans la transition L→O .
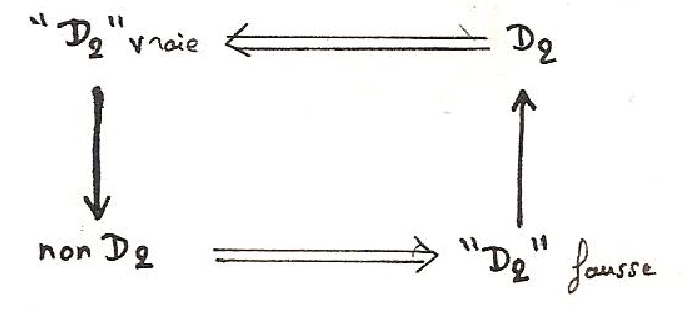 On peut s’amuser à construire un cercle « tournant » en sens inverse, par exemple le casse-tête bien connu du condamné à mort qui sera pendu s’il énonce une proposition fausse et brûlé si elle est juste. Le condamné choisit D2 : « je serai pendu »
On peut s’amuser à construire un cercle « tournant » en sens inverse, par exemple le casse-tête bien connu du condamné à mort qui sera pendu s’il énonce une proposition fausse et brûlé si elle est juste. Le condamné choisit D2 : « je serai pendu »
Le théorème central de Gödel
Nous pouvons désormais nous intéresser directement au théorème central de Gödel[154].
Selon une définition de J.Lardrière, un système formel est « une entité idéale qui fait apparaître (sous forme de « théorèmes ») toutes les conséquences qui découlent selon des critères déterminés (les « règles » du système) d’un certain corps de propositions (les « axiomes » du système). » C’est une entité close, autonome, dans laquelle tout est explicite, construite en vue de représenter une théorie intuitive aux énoncés de laquelle nous attribuons les qualités « vrai » ou « faux » ; aux énoncés « vrais » de la théorie intuitive doivent correspondre les « théorèmes ».
Le théorème de Gödel s’applique à tout système formel S, non contradictoire (impossibilité de dériver à la fois une proposition et sa négation), contenant une représentation de l’arithmétique, et satisfaisant certaines conditions d’effectivité. Il affirme que dans un tel système, il existe au moins une proposition indécidable, D, que nous allons maintenant construire.
Considérons dans S les expressions qui sont les définitions de propriétés d’entiers (prédicats à un argument entier). Ces expressions consistent en systèmes finis de signes (variables et constantes logiques et mathématiques) dont chacun peut être remplacé par un nombre entier arbitraire (choisi judicieusement). On a alors une correspondance entre une expression w mathématique et une suite finie d’entiers.
D’autre part, toute suite finie d’entiers peut être représentée par un nombre entier unique, son nombre de Gödel : par exemple en utilisant la décomposition en facteurs premiers
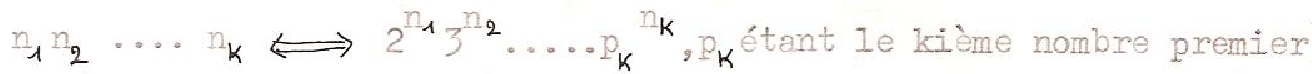 Tel est le principe schématique de la méthode d’arithmétisation de la métamathématique inventée par Gödel, qui permet donc d’établir une correspondance biunivoque entre les expressions de S et les nombres entiers. C’est cette « duplicité » du nombre entier, à la fois argument (objet) et signe qui va rendre possible l’établissement d’un énoncé autoréférentiel D :
Tel est le principe schématique de la méthode d’arithmétisation de la métamathématique inventée par Gödel, qui permet donc d’établir une correspondance biunivoque entre les expressions de S et les nombres entiers. C’est cette « duplicité » du nombre entier, à la fois argument (objet) et signe qui va rendre possible l’établissement d’un énoncé autoréférentiel D :
- Soit Pn le prédicat dont le nombre de Gödel est n.
- Soit la proposition (a) : « p ne possède pas la propriété Pn » ; autrement dit, Pn (p) est fausse au sens de l’arithmétique intuitive. Dans l’optique du langage formalisé, cette proposition devient (b) : « Pn (p) n’est pas dérivable dans S » (i.e. n’est pas déductible des axiomes, conformément aux règles définies à l’intérieur de S). Sous certaines conditions, on vérifie qu’il est possible d’associer à la proposition (b) une expression du système formel, donc un nombre de Gödel, noté Φ(n,p)
- Soit enfin T l’ensemble des nombres de Gödel correspondant à des propositions dérivables (théorèmes) de S.
Considérons maintenant le prédicat: « P (n) n’est pas dérivable dans S », équivalent à
D : 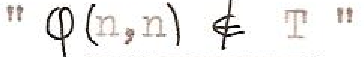 (b’)
(b’)
Le prédicat D correspond à un nombre de Gödel d, car il représente une propriété d’entiers.
Faisons maintenant le dernier pas : appliquons D à lui-même.
D(d) signifie, d’après (b’): 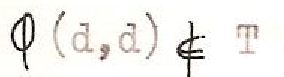 dont le contenu intuitif est « D(d) non dérivable dans S » .
dont le contenu intuitif est « D(d) non dérivable dans S » .
D(d) est donc une expression qui affirme d’elle-même sa propre « fausseté » (dans la théorie intuitive).
Une proposition de S est dite décidable dans S si on peut, soit y dériver cette proposition, soit y dériver sa négation, tout autre cas étant exclu. Montrons que D(d) est indécidable dans S :
 Il serait facile, on le voit, de rapprocher les deux branches et fermer le cercle. Mais sous cette forme, la conclusion du théorème et l’origine du cercle apparaissent clairement :
Il serait facile, on le voit, de rapprocher les deux branches et fermer le cercle. Mais sous cette forme, la conclusion du théorème et l’origine du cercle apparaissent clairement :
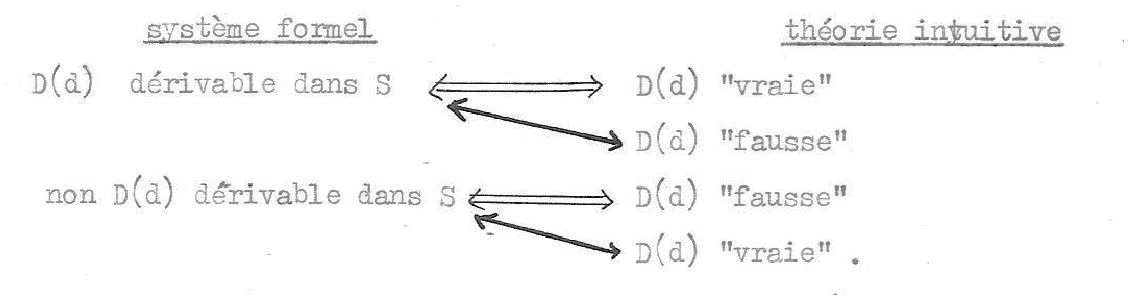 Il n’y a pas de parallélisme complet entre le système formel et le système intuitif, mais une inadéquation irréductible, du fait de l’existence obligée de telles propositions indécidables.
Il n’y a pas de parallélisme complet entre le système formel et le système intuitif, mais une inadéquation irréductible, du fait de l’existence obligée de telles propositions indécidables.
Cependant, une proposition indécidable à l’intérieur d’un système formel S peut être rendue décidable à l’intérieur d’un système plus fort S’, sans qu’on arrive jamais à une représentation parfaitement adéquate[155].
Cet état de fait impose, pour Piaget
« ou bien de concevoir la hiérarchie de toutes les théories possibles comme déjà actualisée en une pyramide d’Idées platoniciennes, mais dont l’inconvénient … est qu’elle est alors, non pas posée sur sa base mais suspendue par son sommet (et l’on ne voit pas trop à quoi, puisqu’il s’agit d’une progression sans fin), ou bien de concevoir cette progression des théories de rang n,n+I, etc, comme appuyée sur un devenir historique [156].»
Cette esquisse rapide d’un problème logique aussi complexe et aussi protéiforme que celui du cercle vicieux, si éloigné de nos habitudes de pensée, n’avait d’autre ambition que de montrer, derrière l’unité des procédés de construction, la grande diversité des stratégies déployées par l’intuition afin de le saisir : images du serpent, du noeud, du miroir figures la dualité, du multiple dans l’un, de la régression, de l’emboîtement, interviennent toutes dans cette lutte angoissante pour cerner l’autoréférence. Pour conclusion, nous ne pouvons que faire nôtre celle de J.Lardrière, dans son magistral article sur Les limites de la formalisation : on y verra combien ces figures sont indispensables à l’expression précise de la pensée :
« ce qui est autoréférentiel comporte une dualité irréductible entre l’acte d’expression et le contenu qui est visé dans cet acte ; il est impossible de rendre le reflétant homogène au reflété, de conférer toute l’actualité d’une opération effective à ce qui n’est que l’index d’une opération virtuelle…
L’acte de thématisation est actuel, il appartient au présent. Mais il vise un terme qui n’est pas actuel, il vise un champ virtuel. Il rabat en quelque sorte sur le présent le champ infini dans lequel ce présent est plongé. Il est donc autoréférentiel en ce sens qu’il reflète dans le présent le présent lui-même…
Mais cette opération autoréférentielle a ses limites : lorsque nous thématisons, nous finitisons l’infini, nous enfermons dans le présent comme domaine déterminé, comme figure fermée, l’extension indéterminée, l’espace illimité d’un horizon. La pensée opératoire est donc incapable d’une réflexion totale : elle ne parvient pas à ressaisir le présent à la fois dans sa limitation et dans son infinité…
elle laisse échapper ce qu’il y a de proprement illimité dans l’infini, tout en conservant cependant quelque chose de cette puissance mystérieuse par laquelle l’infini transgresse irrésistiblement toute limite. »
CONCLUSION
Nous avons dans l’introduction exprimé des réserves quant à la cohérence de la notion de figure de l’intuition que nous nous proposions de dégager. A l’issue de ce travail, les réserves demeurent : s’il existe en effet une certaine analogie entre par exemple la figure du diallèle sceptique et le modèle de prédation de R. Thom, entre le dualisme platonicien et la dualité en mathématiques, il est clair pourtant que ces diverses constructions n’appartiennent pas au même niveau de la pensée, et ce qui les sépare est finalement plus intéressant que ce qui les rapproche. Dès lors, que gagne-t-on à confronter de force aux concepts scientifiques des formes de pensée qui leur sont désormais étrangères, à rappeler à la science des origines parfois douteuses que tout son effort a été justement de répudier ? Nous voudrions en conclusion présenter quelques réflexions rapides sur le statut à attribuer à ces figures intuitives dont la cohérence, en définitive, découle moins de ce qu’elles sont effectivement que du rôle commun qu’elles sont appelées à jouer.
Comment l’homme peut-il connaître de façon certaine le monde, puisqu’il est lui-même partie de ce monde à connaître ? On peut voir plusieurs manières de réfuter ce diallèle épistémologique, par delà le simple fait de l’existence patente de la science.
- Premièrement, nous ne posons jamais au réel une question unique, pour laquelle nous ne pourrions évidemment jamais, dans la réponse, déterminer ce qui provient du monde ou de nous-même ; nous posons une multiplicité de questions, et entre les réponses des corrélations parfois apparaissent. « Tu connaîtras, autant qu’il est possible à un mortel, que la Nature est en tout semblable à elle-même ». Tel est, formulé par Platon, le « principe d’analogie » qui constate ces corrélations et rend possible la science et son avancement, puisque celui-ci procède par englobement au sein de concepts plus vastes, et donc plus justes, de notions auparavant séparées. Les mathématiques sont l’outil par excellence de cette recherche d’analogies, puisqu’elles permettent de cerner, avec quelle efficacité, le minimum commun sous-jacent à la diversité des apparences. Cependant, les figures intuitives que nous avons recensées, à une échelle plus modeste, manifestent le même souci de traquer le semblable sous les espèces du divers. On peut d’ailleurs penser, d’accord avec l’idonéisme de F.Gonseth, qu’il y a continuité entre ces formes plus immédiates de la pensée et les constructions logico-mathématiques, qui en constituent l’aboutissement et la quintessence.
- Deuxièmement, il arrive que des analogies débordent le cadre du monde-objet et semblent impliquer l’esprit lui-même : ainsi, à l’aube de la pensée, la découverte que la nature pouvait être, de la même façon que le langage, structurée en couples de contraires, a pu faire croire à la possibilité d’une influence des mots sur les choses, l’exploration des lois propres au langage remplaçant l’expérimentation directe sur le réel, et le verbe devenant proprement une « formule », au sens d’objet d’une recherche et de sujet d’un calcul. Les figures intuitives marquent l’étape transitoire où la métaphore, déjà détachée du domaine linguistique, n’a pas encore atteint à la pureté du concept scientifique ; Cassirer a magnifiquement décrit ce processus nécessaire d’épuration des concepts :
« ce qui doit prendre vie dans la pensée logique est condamné à mort et à l’engourdissement dans la pensée du langage ; ce qui est pensé ne peut devenir concept qu’en quittant l’état larvaire de sa pré-vie linguistique et en rejetant sa défroque de chrysalide ».
Cependant, de même que le mot et plus tard le concept mathématique, la figure de l’intuition est un signe commun à l’esprit et au monde, puisqu’on ne peut déterminer absolument s’il résulte d’une problématique abstraction à partir des phénomènes, ou de la cristallisation d’une pensée pure qui, inexplicablement, serait adéquate au réel, Analytique ou synthétique, le langage des mots, des formes intuitives ou des formules mathématiques ? On peut rêver en tout cas sur les effets de « moiré » qui se produisent lorsque nous superposons à la trame du monde la trame de nos représentations, sources peut-être de cette esthétique cachée qui guide les grands créateurs ; on peut s’interroger sur les isomorphismes qui rendent nos structures internes aptes à « refléter » assez fidèlement les structures externes : pour R.Thom, c’est aux mathématiques revenues à leur rôle de génératrices d’analogies qu’il appartient d’en élucider la nature :
« c’est à cette tâche d’analyse interne par la modélisation de phénomènes extérieurs que devrait s’attacher la philosophie naturelle. Il y a là une belle partie à jouer pour la science et la philosophie enfin réconciliées ».
Mais les figures intuitives, autre « mixte » commun à l’esprit et au monde, sont peut-être également une clef du réel.
- Car – et ce sera le troisième point de la réfutation du diallèle épistémologique – toute interrogation du réel, toute transaction entre ces deux pôles nécessairement séparés par le procès de la connaissance que sont le monde objectif et l’esprit observant, est à double sens. Construire une théorie explicative, c’est établir entre des faits déjà observés et un modèle mathématique ou logique une analogie que l’expérimentation, lorsqu’elle est possible, doit ensuite valider ou infirmer : si rien ne vient contrecarrer cette analogie, si même celle-ci au contraire en vient à s’étendre sur un plus grand nombre de faits, on considère qu’on a appris quelque chose de nouveau sur le monde ; si par contre un fait résiste à l’englobement, cela remet en cause, non l’édifice mathématique qui reste, dans l’absolu, exempt d’erreur, mais les règles de correspondance, hors formalisation, qui le reliaient au réel observé. Si un simple réajustement du domaine de validité de la théorie ne permet pas de lever la difficulté, il faut en venir à un examen approfondi de ces règles de correspondance, descendant parfois jusqu’à la critique de leurs bases intuitives implicites : le type même de ce processus, assez rare heureusement dans les annales de la science, est bien sûr le bouleversement relativiste. Il arrive alors, ce faisant, que nous apprenions quelque chose sur nous-même et les formes de notre pensée.
Ce processus concerne également les embryons de modélisation que sont les figures de l’intuition, dans la mesure où certaines visent à constituer des systèmes d’explication globale qu’il est donc possible de confronter au réel. Nous pensons ici en particulier aux figures binaires dont le champ explicatif, depuis Héraclite,n’a cessé de rétrécir : si ces figures gardent leur sens en ce qui concerne les phénomènes spécifiquement humains, historiques ou sociaux, si on peut penser les appliquer avec succès à certains phénomènes biologiques de régulation et d’antagonisme, il apparaît qu’elles ne régissent plus grand chose dans les domaines physico-mathématiques :
- en mathématiques, nous avons vu que la notion de dualité ne semble pas réductible à un schéma unique, à moins de perdre tout l’intérêt qui réside justement dans la rigoureuse différenciation des concepts ;
- en logique, les logiques multivalentes ont sonné le glas de la croyance en une dichotomie nécessaire du vrai et du faux : rien dans les lois de l’esprit ne s’oppose à la généralisation, bien que son sens puisse nous échapper ;
- en physique enfin, seules restent marquées du sceau de la binarité des notions difficiles sur les particules élémentaires, qui se diluent de plus en plus au sein d’une effrayante complexité.
Si donc le pouvoir explicatif des figures binaires dans ces domaines semble désormais nul, il n’en reste pas moins crucial de déterminer comment cette vision binaire des choses s’est introduite où elle n’avait pas sa place, pourquoi notre esprit ne peut manipuler commodément que des logiques binaires, pourquoi l’immense majorité des opérations et des relations mathématiques sont binaires, quelles sont les propriétés émergentes ou évanouissantes lors de la généralisation d’un concept binaire. Désormais, l’objet d’étude ici n’est plus le monde,mais l’esprit de l’homme.
Ainsi donc, le diallèle épistémologique sous sa forme brutale n’est plus recevable, mais il n’y a pas d’interrogation infructueuse : les erreurs ou les apories apportent autant que les démonstrations sans faille, à condition de savoir renverser l’objet de l’interrogation. Nous n’en voulons pour exemple que la figure justement du cercle vicieux, devenue après des siècles de répulsion un objet propre d’étude, qui a permis la naissance de la difficile théorie des modèles et l’évaluation des possibilités de formalisation de l’esprit.
Cependant, l’intérêt principal des figures de l’intuition ne réside plus dans le progrès de la connaissance, puisque les formes plus performantes des concepts mathématiques les ont désormais remplacées : il est dans l’approfondissement de notre compréhension. De plus en plus en effet, on voit se distinguer le connaissable et le compréhensible. La science sur son erre découvre constamment des phénomènes que nous ne saisissons plus que de très loin, au travers d’instruments physiques ou mathématiques complexes, au prix d’une discipline intellectuelle contraignante. Nous les connaissons, mais seuls des individus exceptionnels peuvent prétendre à la compréhension à leur égard, dans la mesure où comprendre signifie « faire sien ». Comme le remarque Cassirer à propos du concept scientifique, « ce qui manque à cette formule en proximité de vie et en plénitude universelle, elle le remplace de l’autre côté par l’universalité de son extension et par sa validité générale « . Ainsi, au fur et à mesure que nous nous rapprochons d’une appréhension plus exacte du monde, devons-nous en quelque sorte « chosifier » notre pensée, l’astreindre à des tâches qui ne lui sont pas familières.
Les figures de l’intuition sont à l’opposé, sur cette chaîne de la connaissance qui se tend entre le monde et l’esprit : du côté de l’homme. Elles sont les formes sous lesquelles il lui est habituel et commode d’analyser le réel. Cependant, il semble judicieux d’éviter d’employer à leur égard le terme de « structure », qui sous-entendrait quelque chose de figé, d’inhérent à la conformation même de notre entendement : elles sont plutôt la résultante complexe et changeante, certes de certains mécanismes intellectuels, mais aussi d’habitudes éducatives, de réminiscences d’impressions vécues, d’influences reçues : qui pourrait nier par exemple que certains esprits sont fascinés au delà du raisonnable par l’idée de l’opposition binaire des choses, tandis que d’autres aspirent à une harmonie universelle, certainement tout aussi étrangère au réel. Les figures de l’intuition sont véritablement des figures de style, de style de pensée, qui comme telles peuvent verser dans une rhétorique stérile lorsqu’on en vient à préférer l’élégance des formes à la consistance des faits, mais tout aussi bien procurer d’éblouissants éclairs de compréhension véritable. Elles sont ce qu’il y a de plus humain dans le processus de la connaissance puisque, métaphores, elles appartiennent au langage commun ; puisque, figures géométriques simples, elles appartiennent au fonds imagier le plus universel.
Par là, elles sont appelées à jouer un rôle capital pour la compréhension : on peut en effet avancer que celle-ci passe le plus souvent par des figures de ce stype – abandonnées ensuite au profit d’autres plus élaborées et plus performantes – mais qui restent toujours un recours : il est significatif de voir comment dans les domaines où la science se heurte à un cruel défaut de données expérimentales, comme par exemple en cosmogonie, les modèles d’univers proposés dépendent tous, à la base, de telles figures intuitives : temps cyclique ou linéaire[157], espace en dilatation/contraction ou en expansion indéfinie… De même, les difficultés apparues dans l’étude des particules élémentaires pourraient, selon certains, être levées au prix de la révision d’une notion aussi immédiate que celle de séparabilité, c’est-à-dire de frontière[158].
Quoiqu’il en soit, il apparaît que si, pour les progrès de la connaissance elle-même, on peut généralement ignorer les figures de l’intuition, il n’en est pas de même lorsqu’une étape de compréhension s’impose : lors de la constitution de concepts scientifiques nouveaux, ou lors de l’acquisition par l’individu de connaissances nouvelles, pour lesquelles il doit forger sa propre représentation. A cet effet, une meilleure utilisation des principales figures, en liaison avec les acquis de la psychologie génétique, pourrait sans doute jouer un rôle pédagogique important.
Mais ne risque-t-on pas, ce faisant, de ressusciter une gnose ou une scholastique funeste, une forme brumeuse du savoir pour ceux qui ne pourraient pas jusqu’au bout parcourir la chaîne du connaître ? Nous pensons que ce danger est moindre que de voir une science délaisser l’explication pour la description, et les non-scientifiques renoncer à comprendre ce qu’ils ne peuvent savoir absolument. Car comprendre est un besoin de l’esprit qui, non satisfait, mène à la crédulité et à la superstition; qui, trop bien satisfait, stérilise la pensée ; mais qui, convenablement satisfait, pousse l’esprit à apprendre davantage.
Le Descartes des Principes de la philosophie pouvait prétendre avoir « compris » le monde, au sens d’avoir « éteint son doute ». Bien que la science ultérieure ait fort peu retenu de son système, il n’en a pas moins sa place au sein de l’histoire des idées, en tant que construction dont on sait qu’elle est inexacte, mais riche en pouvoir de séduction et en enseignements possibles. Car si l’exactitude, c’est-à-dire l’adéquation au réel, est un idéal unique, la compréhension, c’est-à-dire l’intégration du monde au sein de soi, est affaire avant tout de convenance personnelle : cette non-univocité des modes de compréhension est sans doute la leçon fondamentale de la philosophie de Leibniz : il n’y a qu’un seul monde et une seule vérité, mais à chaque monade en est échue, par sa nature propre, une compréhension différente.
BIBLIOGRAPHIE
R. Arnheim. La pensée visuelle. Flammarion 1976.
E.Bernard-Weil, L’arc et la corde : un modèle d’antagonismes dialectiques en biologie et dans les sciences humaines, Maloine 1975.
L. von Bertalanffy, Théorie générale des systèmes.
E. Bitsakis. Physique contemporaine et matérialisme dialectique. Ed. Sociales, 1973.
C.P.Bruter.
- Topologie et perception. T I, Maloine, 1974.
- Sur la nature des mathématiques, Gauthier-Villars, 1973.
H R. Carnap, Les fondements philosophiques de la physique, Armand-Colin, 1973.
M.Carvallo, Logique à trois valeurs, logique à seuil, Gauthier-Villars, 1968.
E.Cassirer, Philosophie des formes symboliques, T I et III, Ed.de Minuit, 1972.
J.Cavaillès, Philosophie mathématique, Hermann, 1962.
J.E. Charon,
- L’esprit, cet inconnu, Albin Michel, 1977.
- Le monde éternel des éons, Stock, 1980.
C. S. Chihara, Ontology and the vicious circle principle. Cornell U.P., 1973.
Cohen, Les origines de la physique moderne, Payot
JEJ.Daetwyler, Sciences et arts. Une contribution à l’étude des structures et des sources des arts et des sciences, La Baconnière, Neuchatel, 1972.
M.Desmarest.M. Druel, La ternarité, Courrier du Livre, Paris, 1976.
P.Destouches-Février, Structure des théories physiques, PUF,1951.
G. Durand, Structures anthropologiques de l’Imaginaire, PUF, 1963.
V.Fritsch, La gauche et la droite, vérités et illusions du miroir, Flammarion, 1967.
F.Gonseth, Les mathématiques et la réalité, Paris, Blanchard, 1974.
I.J.Good. Quand les savants donnent libre cours à leur imagination, Dunod, 1967.
S. Haack. Deviant logic, Cambridge U.P.
J.Hadamard, Essai sur la psychologie de l’invention dans le domaine mathématique, Gauthier-Villars, 1975.
F.Halbwachs, La pensée physique chez l’enfant et le savant. Delachaux-Niestlé, Neuchatel, 1974
D.Hilbert. S. Cohn Vossen, Geometry and the imagination, Chelsea, New-York 1932.
E. Kasner.J.Newman. Les mathématiques et l’imagination, Payot, 1950.
A.Kaufmann, Introduction à la théorie des sous-ensembles flous, t 1,1973.
A.Koestler,
- Le cri d’Archimède. (The act of Eration creation). Calmann-Lévy, 1965.
- Le cheval dans la locomotive, Calmann-Lévy, 1968.
A.Lautman, Essai sur l’unité des mathématiques, 10/18,1977.
G.Leibniz, Monadologie.
S.Lupasco,
- Logique et contradiction, Presses Universitaires, 1947.
- Les trois matières, 10/18, 1970.
B.Mandelbrot, Les objets fractals, Flammarion, 1975.
A. Mercier, G.Rüttman, Le problème posé à la logique par l’apparition des théories quantiques. In Etudes Philosophiques, N°4, 1969.
Moisil, Essai sur les logiques non-chrysipiennes. Ed. Académie de la Rep. Pop. De Roumanie, Bucarest, 1972.
J.Piaget,
- Essai sur les transformations des opérations logiques. Les 256 opérations ternaires de la logique bivalente, PUF, 1952.
- (sous la direction de) Logique et connaissance scientifique, Pleiade 1969.
E.Morin, La méthode, t I, Seuil, 1977.
A.Mostowski. Sentences indecidable in formalized arithmetic. An exposition of the theorie of Kurt Gödel. North Holland Publishing Company, Amsterdam 1964.
G.Poulet, Les métamorphoses du cercle, Flammarion, 1979.
B. Russell,
- Introduction à la philosophie mathématique, Payot, 1928.
- La méthode scientifique en philosophie, Payot.
- Histoire de la philosophie occidentale en relation avec les évènements politiques et sociaux de l’Antiquité jusqu’à nos jours, Gallimard, 1968.
M. Serres,
- La naissance de la physique dans le texte de Lucrèce :fleuves et turbulences, ED.Minuit.1977.
- Le système de Leibniz et ses modèles mathématiques, PUF, 1968.
R.Thom,
- Morphogénèse et imaginaire. Cahiers de recherche sur l’imaginaire. N°8-9, 1978. Unesco.
- La pensée scientifique. Quelques concepts, démarches et méthodes. Mouton, 1978.
– A.Virel, Histoire de notre image, Ed. du Mont Blanc, Genève, 1965.
– J.Voilquin, Les penseurs grecs avant Socrate, Garnier-Flammarion, 1964.
– P.A. Weiss, L’archipel scientifique, Maloine, 1974.
– H.Weyl, Symétrie et mathématiques modernes, Flammarion, Nouvelle Bibl. Scient.
Table des matières
Exemples de « frontières » dans les domaines scientifiques 9
Exemples de « frontières » hors des domaines scientifiques 12
FIGURES DE L’UN : LE CERCLE, LA SPHERE 16
Métaphores et modèles sphériques 18
Le cercle,métaphore de l’éternité 18
La sphère, figure trinitaire 18
La sphère sénaire d’Abellio. 20
Le « module cosmique » de G.Lacroix 20
L’échappée dans l’ailleurs. 38
L’échappée temporelle : la dialectique. 39
La binarité déchue. Passage au continu. 43
L’analytique et le synthétique 44
Logique trivalente (Post, Lukasiewicz, 1920) 46
La dualité et ses paradoxes. 50
Le circulaire et le linéaire. 52
Annexe I : La monade et ses avatars 58
Origines de la monade leibnizienne 58
Caractéristiques du modèle monadique 59
La monade comme point de vue. 62
La monade comme Multiple dans l’Un 62
La monade comme palimpseste 64
Annexe II : La dualité en mathématiques. 67
Dualité en logique bivalente. 69
Dualité en géométrie projective. 70
Dualité au sens des formes linéaires. 71
Dualité dans la théorie des catégories. 72
Annexe III : La méthode de la diagonale et la construction de cercles vicieux 73
Thématique du cercle vicieux. 73
Formation d’un mixte autonome 74
« L’ensemble de tous les ensembles » 80
« L’ensemble des ensembles qui n’appartiennent pas à eux-même » 80
Du paradoxe du menteur au théorème de limitation de Gödel 84
Le théorème central de Gödel 87
11
- Cité par Koestler, Le cri d’Archimède, p 306. ↑
- En fait de monographie sur l’une de ses figures, nous avons trouvé seulement : D.Mahnke, Unendliche Sphäre und Allmittelpunkt, Halle 1937 et G.Poulet, Les métamorphoses du cercle. Flammarion 1979 ↑
- Cassirer, Philosophie des formes symboliques, Tome I, p 7. ↑
- Serres, Le Système de Leibniz et ses modèles mathématiques, p 286. ↑
- Par exemple Binet, La psychologie du raisonnement, 1886. ↑
- Descartes, Regulae ad directionem ingenii. ↑
- Cassirer, tome I, p 32. ↑
- Cassirer, tome II, p 411; d’après Fraenkel, « I° leçon sur les fondements des mathématiques ». ↑
- Construction donnée dans Kasner-Newman,p 202. ↑
- D’un point de vue terminologique, « limite » met l’accent sur l’aspect potentiel (f « tend » vers une limite) de la notion que nous évoquons, et « frontière » sur son aspect actuel (f prend une valeur sur la frontière, effectivement atteinte).Ces deux aspects coïncident lorsque f est supposée continue sur le domaine considéré, ce qui est le cas le plus fréquent pour l’intuition. ↑
- Sur cette question du point de vue local ou global en analyse, voir Lautman,p 38 ↑
- M.Merleau-Ponty. Cosmologie du XX° siècle, NRF 1965,p 35. ↑
- Lanza del Vasto, Principes et Préceptes du Retour à l’Evidence, p 39. ↑
- Cité par Russell, Histoire de la Philosophie Occidentale ↑
- Cité par Voilquin, p 95 ↑
- Cité par Russell, Histoire de la Philosophie Occidentale, p 75 ↑
- Bachelard, Formation de l’esprit scientifique,p 98 ↑
- Spinoza, Ethique, I, prop XI ↑
- Cité par Arnheim, p 96 ↑
- Freud. Civilisation and its discontents, p 13. Cité par A.Koestler, Cri d’Archimède, p 275, qui voit dans ce sentiment océanique l’expression de la « tendance à l’intégration » du holon (voir note 150). ↑
- Cassirer, tome III,p 50 ↑
- G. Canguilhem, Connaissance de la vie, p 167. ↑
- Nous pensons notamment aux études de Jung sur les mandalas hindoues, considérées comme des figurations unitaires de la psyché. ↑
- Cité par Cohen, Les origines de la physique moderne, Payot, p 124. ↑
- Sur cette conjonction dans la figure de la sphère de l’indétermination et de la détermination par un maximum, voir le développement de M. Serres, p 201. ↑
- Cette conception du cosmos comme une sphère reprend celle de Parménide. ↑
- Schopenhauer, Métaphysique de l’amour, métaphysique de la mort. Ed. 10/18, p 116. ↑
- St Thomas d’Aquin. Cité par Poulet, p 28. ↑
- Kepler. Cité par R. Arnheim, p 291. Les métaphores qui suivent sont également empruntées à cet ouvrage. ↑
- Sur cette analogie, voir A.Koestler, Le cri d’Archimède, p 111 ↑
- Cette intuition d’une sorte de rayonnement (le Saint Esprit) occupant l’espace entre centre et surface extérieure, se retrouve dans la conception de Halley selon laquelle la Terre serait un système solaire en miniature, possédant un noyau intérieur et une coquille externe ; entre les deux régnerait un fluide lumineux, éclairant d’un côté les êtres vivants à la surface du noyau, et s’échappant de l’autre par les pores de la coquille en effluves lumineuses : les aurores boréales. Cité par A.Koestler, Le cri d’Archimède, p 395. ↑
- D’après R.M.Mosse-Bastide, Pour connaître la pensée philosophique de Plotin,p 61,114. Il existe cependant chez Plotin une conception trinitaire, la triade de l’Un, de l’Intelligence et de l’Ame. Le rayonnement qui émane de l’Un, se retourne vers lui et devient l’Intelligence, qui rayonnant et se convertissant à son tour devient l’Ame. Mais cette ternarité ne semble pas explicite dans le modèle de la sphère. ↑
- R. Abellio, La structure Absolue. Citations p 22. Schéma p 47. ↑
- G.Lacroix, Théorie de la dialectique cosmique. Lauzeray international, 1979. ↑
- Giordano Bruno, De triplici minimo, I, III. Cité par M.Serres. ↑
- Arnheim, p 291. Poulet, p. 38. ↑
- Cité par Kasner et Neuman, ↑
- R. Thom, p 77. ↑
- Pour l’historique de cette métaphore, :voir Dietrich Mahnke, Unendliche Sphäre und Allmittelpunkt, Halle, 1937. ↑
- Cette curieuse conception de l’air comme l’océan d’un monde supérieur a été reprise notamment par l’écrivain fantastique américain Ch. Ford, Le livre des Damnés. ↑
- La propriété mathématique qui semble prépondérante ici est celle d' »homothétie interne », la figure étant semblable à elle-même par un ensemble d’homothéties. ↑
- Tout comme celle des sphères gigognes, cette figure se caractérise par des homothéties internes. Il semble qu’il existe une liaison intuitive forte entre cette ressemblance interne de la figure avec ses parties, et la reproduction indéfinie du semblable qui caractérise les phénomènes vitaux. Ainsi, trois siècles après Leibniz,le mathématicien Cesaro retrouve des accents préformationnistes dans sa description de la courbe de Von Koch (cité par Mandelbrot, Les objets fractals, p 29 : « c’est cette similitude entre le Tout et la partie,même infinitésimale, qui nous porte à considérer la courbe de Von Koch comme une ligne merveilleuse entre toutes. Si elle était douée de vie, il ne serait pas possible de la supprimer d’emblée, car elle renaîtrait sans cesse des profondeurs de ses triangles, comme la vie dans l’univers ». ↑
- Serres, p 370. ↑
- Voir le schéma et la légende de Fournier dans B.Mandelbrot, Les objets fractals, Flammarion 1975, p 79 https://archive.org/details/lesobjetsfractal0000mand/page/79/mode/1up : « ce diagramme est utile car il montre qu’une hiérarchie infinie d’univers peut exister sans que le « ciel soit de feu » Si les plus petits points visibles représentent les atomes de l’inframonde, la figure entourée d’un cercle représentera une étoile de l’infra-monde, c’est-à-dire un atome du nôtre. Le cercle A correspondra à une étoile de notre-monde… » (Remarquons que la projection de cette figure sur un de ses axes donne un ensemble de points analogue au discontinu de Cantor. Voir notre chapitre III, note 10.). ↑
- Cité par Von Bertalanffy. Théorie générale des systèmes, p 233. ↑
- Cité par A. de Benoist, Vu de Droite, p 162. ↑
- Serres, p 751 et suivantes. ↑
- La figure de l’étoile est bien sûr utilisée en optique, pour symboliser une source de lumière ponctuelle isotrope. Bachelard (Activité rationaliste de la Physique contemporaine,p 88) fait remarquer que la figure complète se compose de deux figures duales, les droites des rayons et les sphères orthogonales des fronts d’onde, qui se propagent vers l’extérieur. ↑
- Berkeley, Cours de physique, t 2, p 165 ↑
- Serres, p 14 ↑
- Thom, p 77. ↑
- C.P. Bruter, Sur la nature des mathématiques, p 35 ↑
- C.P. Bruter, Topologie et perception, p 37. ↑
- Lanza del Vasto. Enfances d’une pensée, p 19. ↑
- C.G.Hempel, International Encyclopaedia of unified science. Vol 2, N°7. Chicago, 1952. cité par A.Koestler,Le cri d’Archimède. ↑
- Cassirer, t I, p 53 ↑
- Nous résumons le paragraphe : Relations multiple-un, Serres, p 151 et suivantes. La construction leibnizienne d’ailleurs ne s’arrête pas là. Rabattant en quelque sorte l’axe de la vision divine parmi le réseau des perceptions intermonadiques (puisque Dieu est lui-même une monade), on doit conclure que ce point unique, ce point géométral, est en réalité « partout situé » dans le réseau. L’espace métaphysique des monades, polycentrique, continu homogène de points de vue hétérogènes, est désormais complètement constitué. ↑
- Kant, Critique de la Raison Pure ,p 453. Cité par Cassirer,p 526. ↑
- Cassirer, t I,p 23. ↑
- Serres, paragraphe : Le paradigme pascalien, p 648 et suivantes. ↑
- Cassirer, t III, chapitre 6. ↑
- Pascal voyait dans la latéralité de l’homme l’origine de la notion de symétrie. ↑
- Des expériences de psychologie ont montré l’anisotropie des directions horizontales et verticales dans l’espace perspectif et visuel humain (Von Allesch, Skramlik…….). ↑
- Schopenhauer. Théorie des couleurs. Cité par Frisch,p 24 ↑
- L’exclusion mutuelle des deux descriptions est, on le sait, très controversée. Louis de Broglie a d’ailleurs contesté en son temps le caractère pertinent de la notion de complémentarité : « elle ne constitue aucunement une explication et les extrapolations qu’on a cherché à en faire en dehors du domaine de la microphysique paraissent extrêmement périlleuses. » (Les représentations concrètes en microphysique, in Piaget ,1969, p 713 ). Exemple d’extrapolation oiseuse : alternative entre observer un animal vivant (biologie) ou mort (biochimie). ↑
- Lupasco 1979, p 31 .Le physicien et philosophe américain A. Shimoni propose lui aussi un retour à la terminologie aristotélicienne pour décrire les phénomènes microphysiques. ↑
- Lupasco 1970, p 172. ↑
- Lupasco 1970,p 89. Pour compléter ce résumé très incomplet de la néo-scholastique de Lupasco, ajoutons qu’elle s’organise autour d’un autre couple de notions : homogénéisation et hétérogénéisation, la première liée au Second principe de la Thermodynamique la seconde au Principe d’Exclusion de Pauli. Il en résulte la trichotomie :matière macrophysique, correspondant à l’homogénéité
matière vivante, correspondant à l’hétérogénéité
matière microphysique, correspondant à un intermédiaire
L’originalité est que le « troisième terme » (microphysique), plutôt que de surpasser et de « coiffer » les deux autres, est au contraire le substrat, l’étoffe commune aux deux. ↑
- Koestler, Le cri d’Archimède ‚p 32. ↑
- Serres, 1968, p 121 ↑
- Citons par exemple le procédé de construction du « discontinu de Cantor », par trichotomie : on divise en trois l’intervalle [0, 1], dont on ôte la partie centrale ]1/3, 2/3 [ ; on opère de même sur chacun des intervalles restants, et en itérant indéfiniment, on aboutit à un ensemble de points discontinus, les nombres triadiques. Une autre application très particulière de la division par trois est la démonstration de la non-dénombrabilité du segment réel [0, 1] : supposons que tous ces réels puissent s’ordonner en une suite X = x1, x2… xn. Divisons [0, 1] en trois et choisissons parmi les trois intervalles celui qui ne contient pas x1 , soit [p1, q1]. En itérant cette opération, on obtient une infinité de segments emboîtés [pn, qn] convergeant vers un nombre x, qui par construction n’appartient pas à la suite X. Cette démonstration constructiviste est antérieure à belle par la méthode de la diagonale que nous présentons en Annexe III : La méthode de la diagonale et la construction de cercles vicieux. La division par trois est impérative : dans le cas d’une division par deux, il pourrait être impossible de choisir un intervalle ne contenant pas x , lorsque celui-ci se situerait sur la frontière. ↑
- Pour Boole, la réunion ne pouvait être définie que dans le cas de classes disjointes. Voir Piaget, 1969, p 159. ↑
- Logique de Port-Royal III,I ↑
- Lautman, p 106. ↑
- Descartes, Traité des Passions de l’âme. Art 31,32. ↑
- Koyré. Du monde clos à l’univers infini. ↑
- Lanza del Vasto. La trinité spirituelle, p 182. ↑
- Lanza del Vasto. Enfances d’une pensée, p 104. ↑
- Bitsakis, p 195. ↑
- Althusser, Sur le rapport de Marx à Hegel. ↑
- L.Mumford, Technique et civilisation. ↑
- Schleicher, Sprachvergleichende Untersuchungen (1848). Cité par Cassirer,t I,p 114. Schleicher pensait que sa classification n’était pas seulement analogique,mais émanait objectivement de l’essence même du langage. ↑
- A.Virel, Histoire de notre image. ↑
- M.Gardner. Pour la science. Sept 78, No 11 ↑
- Il est passionnant de suivre, depuis « Enfances d’une pensée » jusqu’à « La trinité spirituelle » le développement de cette intuition trinitaire, dont la précocité et la permanence prouvent qu’elle préexiste à toute construction rationnelle. ↑
- A l’appui de cette thèse, citons cette opinion parallèle de S.Petrement (in Le dualisme chez Platon, les Gnostiques et les Manichéens, PUF 1947) : « c’est toujours par quelque théorie d’apparence dualiste que la philosophie s’éveille, tandis que les systèmes monistes viennent toujours un peu plus tard, comme un apaisement, une conciliation qui est aussi, dans une certaine mesure, un affaiblissement et le commencement d’une décadence. » ↑
- Cité par Russell, Hist. Philo. Occid. p 83.Voir aussi J.P. Dumont, Le scepticisme et le phénomène.p 233. ↑
- Leibniz. Essais, avant-propos. ↑
- Serres p, 128. ↑
- Koestler. Le cri d’Archimède.P 396. ↑
- Exposé par H.Weyl, p 45. ↑
- H. Weyl, Raum, Zeit, Materie, 1918. ↑
- Piaget, 1969 p 90. ↑
- Piaget, 1969, p 427.Sur le problème analytique/synthétique : en faveur de la distinction, Carnap,Les fondements philosophiques de la physique,p 249. contre la distinction: Quine, Two dogmas of empiricism. Pour un exposé récent du problème J.Largeault. Enigmes et controverses. Aubier 1980 p 25. ↑
- Mentionnons, à l’intérieur de la logique bivalente, un autre type de généralisation exposé dans Piaget. Essai sur les transformations des opérations logiques. PUF 1952. Il existe 4 opérations uninaires s’appliquant à une seule variable logique p, qui lui associent respectivement p, p (non p), 0 ou 1 (p ou p). Lorsqu’on passe à deux variables p et q, on dénombre 16 opérations binaires lesquelles on peut définir certaines transformations ( I, R, N, C) formant, entre autres propriétés, un groupe commutatif. C, par exemple (Corrélative) consiste à permuter les « et » et les « ou » dans l’expression de l’opération. Peut-on généraliser ces résultats aux 256 opérations ternaires, c’est à dire prenant en compte dans leur expression trois variables logiques ? On constate d’abord que ces opérations sont décomposables en produit de deux opérations, soit uninaire-binaire, soit binaire-binaire. Quant aux transformations de ces opérations, elles forment des structures beaucoup plus compliquées que le groupe IRNC, notamment des treillis. Piaget rappelle que si la notion de groupe est psychologiquement liée à la notion de réversibilité ( x + (-x) = 0 ), la structure de treillis se réfère aux notions de classification et d’inversion d’un ordre. Le passage des opérations binaires aux opérations ternaires confirme donc cette « double parenté » de la pensée logique. ↑
- Von Neumann et Birkhoff ont cependant montré que la structure des propositions quantiques, contrairement à la logique classique, est un treillis non-distributif. Voir par exemple Lautman, p 251. ↑
- Nous n’avons pas mentionné, parmi les logiques s’affranchissant du principe du Tiers-Exclu, les logiques intuitionnistes : on sait que certains mathématiciens ont renoncé à attribuer une valeur vraie ou fausse à des énoncés pour lesquels il n’était pas possible de construire, de manière finie, une règle effective de décision. Pour ces mathématiciens constructivistes, des démonstrations telles que celles basées. sur le raisonnement de la diagonale (voir Annexe III : La méthode de la diagonale et la construction de cercles vicieux), qui impliquent la considération d’un infini actuel et une preuve par l’absurde, ne sont pas valides : le principe du Tiers Exclu, défini uniquement pour des collections finies, ne saurait s’appliquer à de telles situations. ↑
- Russell, Principles of Mathematics, p 205, paragraphe 194. ↑
- Voir R.Thom, p 48. ↑
- Voir par exemple Spinoza. Ethique. Livre I, prop.15. ↑
- H. Weyl, p 43. ↑
- St Thomas d’Aquin. Summa theologica II,85,6. ↑
- Pour un exposé polémique de ces thèmes, voir par ex. A. de Benoist. Vu de droite, p 298. ↑
- Serres,p 226. ↑
- Signalons encore, à propos.de ce schématisme, l’étude de Bachelard (Matérialisme rationnel,p 193-206) sur l’ordre des couleurs du spectre. Tandis que la physique impose un ordre linéaire, les conditions biologiques de la perception, basées sur les trois couleurs fondamentales, conduisent à un ordre circulaire. ↑
- Discuté et réfuté dans la Logique de Port-Royal, III chap. 19. ↑
- Descartes. Principes de la philosophie. II, 33. ↑
- Le chimiste Kékulé, découvreur de la structure cyclique du benzène, assure que l’idée lui en vint lors d’un rêve, ou l’ouroboros se manifeste dans une curieuse réminiscence : « Les atomes continuaient de gambader devant mes yeux de longues rangées parfois étroitement ajustées, le tout avec des ondulations et contorsions de serpent. Mais soudain, que se passe-t-il ? L’un des serpents a saisi sa queue, et la forme s’est mise à tourbillonner de façon moqueuse sous les yeux. Comme en un éclair, je m’éveillai. Apprenons à rêver, messieurs. » Cité par Koestler, Le cri d’Archimède. ↑
- Koestler, La corde raide p 106. ↑
- Husserl. Idées directrices pour une phénoménologie p 312.Cité par Cassirer, t III, p 224. ↑
- E.Morin.La méthode ti,p 18, 19.Le parti-pris de la circularité revêt parfois dans cet ouvrage un caractère obsessionnel : voir notamment le paragraphe « La grande roue »: « tout ce qui est existence, tout ce qui est organisation active fait la roue » ↑
- R.Thom.p 43. On trouvera également une comparaison de ce modèle de prédation avec les catégories dégagées par G. Durand dans ses « Structures anthropologiques de l’Imaginaire ». ↑
- Voir Serres,p 209. ↑
- Leibniz, Monadologie, paragraphe 56. ↑
- Leibniz, Monadologie, paragraphe 57 ↑
- Leibniz, A Sophie. ↑
- Serres, p 747. ↑
- A.Lautman,p 49. ↑
- D’après J.E. Charon, L’esprit, cet inconnu, A.Michel ,1977 et Le monde éternel des éons, Stock, 1980. ↑
- Charon, 1977.p 95. ↑
- Charon, 1980, p 146. ↑
- Serres, p 448 et suivantes. ↑
- Charon, 1977,p 177. ↑
- Charon, 1980, p 83. ↑
- Cassirer, t I, p 107. ↑
- Pour l’exposé rigoureux de cette théorie logique, et le parallèle avec la Monadologie, voir J.Vuillemin, La logique et le monde sensible,p 108. ↑
- Merleau-Ponty. Cosmologie du XX siècle, NRF 1965, p 187. ↑
- Lautman, p59. ↑
- I.Prigogine et I.Stengers, La dynamique de Lucrèce à Leibniz, Critique, 1979. ↑
- Pour un exposé plus technique de ces notions, voir Prigogine, Physique, temps et devenir, Dunod 1980, p 41 et 69. ↑
- G.Gale. Chew’s monadology. Journal of History of Ideas, vol. XXXV, apr-jun 74, p339-348. ↑
- On connaît l’influence croissante sur certains physiciens contemporains, confrontés à ces difficiles problèmes de la non-séparabilité, de la pensée orientale. Ainsi F. Capra (Colloque de Cordoue, 1980, p 52) cite à l’appui de sa conception du monde ce passage, typiquement monadologique, d’un texte sacré hindou : Dans le ciel d’Indra se trouve, dit-on, un réseau de perles, arrangé de telle sorte que lorsqu’on en regarde une, on voit toutes les autres qui se reflètent en elle. Semblablement chaque objet dans le monde n’est pas seulement lui-même, mais comprend chacun des autres et est en fait tous les autres. » ↑
- Serres, p 104. ↑
- Wilson, Sociobiology, the new synthesis. Harvard, 1975. Cité par P.0.Hopkins, La Recherche, No 75. ↑
- Charon, 1980, p 197. ↑
- Schopenhauer, Métaphysique de l’amour,métaphysique de la mort. Ed. 10/18. ↑
- M.Stirner, L’Unique et sa propriété. ↑
- C.P. Bruter ,1973, p 119. ↑
- Russell, 1928 ↑
- Russell, 1928 ↑
- Dedekind, Les nombres; que sont-ils et à quoi servent-ils?, Omnicar. Théorème 66. voir aussi Cavaillès,p 125. ↑
- Thom 1978, ↑
- Une démonstration antérieure (1873) de Cantor utilisait uniquement les propriétés de densité et de compacité du continu réel, en construisant des intervalles emboîtés convergeant vers un élément extérieur à la suite initiale. Voir Cavaillès,p 74,et notre chapitre FIGURES BINAIRES . ↑
- Dedekind emploie ailleurs une méthode de « fusionnement » : à partir d’une série de fonctions Ψn(n) déterminées de manière univoque pour chaque entier n, il construit sur N la fonction Ψ définie par Ψ(n)=Ψn(n), pour chaque n. Cavaillès (p 133) y voit l’analogue de la méthode de la diagonale : « dans les deux cas, on définit une nouvelle fonction d’après l’ensemble des valeurs des fonctions d’une série pour l’argument égal à leur numéro d’ordre, ici (fusionnement) unissant toutes les fonctions, là distinctes d’elles toutes. » ↑
- Ce qu’il faut entendre par « définie », et les améliorations à cet axiome apportées ultérieurement sont exposées par Cavaillès, p 114 et suivantes. ↑
- Recherches de Botvar, Fitch. Voir Piaget 1969, p 237 ↑
- Selon Chihara,p 20.Pour A.Mostowski, au contraire (in « La pensée scientifique, ed. Mouton, 1978, Unesco), les ordres sont définis à l’intérieur des types, de manière à échapper à chaque niveau à des cercles vicieux. ↑
- Si α et β sont les catégories de x et y, alors par définition la fonction f : x→ y appartient à une catégorie du système, notée fα β .On trouvera une introduction à ces notions dans la contribution de J.Lardrière in « L’explication dans les sciences », Flammarion 1973,p 41. ↑
- Gonseth, p 255. ↑
- A.Koestler, 1968, p 58.L’activité et la passivité sont deux déterminations approchées : plus exactement « la tendance à l’affirmation de soi du holon exprime la totalité et la tendance à l’intégration en exprime la parcelléité. » ↑
- Cité par Chihara,p 141. ↑
- Nous donnons ici la variante du paradoxe due à A.Mostowski. On trouvera dans Chihara,p 139,le même paradoxe obtenu par application de la méthode de la diagonale aux décimaux entre 0 et 1, classés selon leur définition en anglais. Dans Kac et Ulam, Mathématiques et logique, on lit un paradoxe semblable, s’appliquant aux fonctions « calculables » f(n), c’est à dire telles qu’il existe une proposition contenant un nombre fini de mots qui permet le calcul de f(n) par un nombre fini d étapes. ↑
- Piaget,p 328 ; J.Lardrière, Les limites de la formalisation. 1969. ↑
- Nous suivons ici la démonstration simplifiée donnée par Mostowski, op. cit. ↑
- Le seul moyen d’assurer l’adéquation parfaite du système formel est de considérer tous les modèles qui lui sont associés, et non un seul comme dans le théorème de Gödel. Ceci démontre, selon l’expression de J.Lardrière « une sorte de surdétermination du système formel, qui le rend susceptible d’une grande variété d’interprétations, qui le rend donc incapable de représenter adéquatement la démarche de la pensée intuitive » (p323) ↑
- Piaget, p 117, 1969. Cette image est sans doute inspirée de celle du Songe de Théodore chez Leibniz, qui présente la pyramide des mondes possibles, mais suspendue en haut au Meilleur des Mondes Possibles. Trois siècles séparent ces deux visions, 1’une qui appelle de ses voeux un point culminant, un point fixe, l’autre qui pense sans effroi la régression à l’infinie, conçue désormais comme une Histoire. ↑
- Gödel, en dehors de ses recherches métamathématiques, a proposé un modèle d’univers « paradoxal »‚ à temps circulaire ↑
- Allusion à l’intrication quantique, qui sera prouvée par l’expérience d’A.Aspect en 1982, un an après la rédaction de ce mémoire. ↑


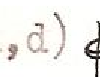

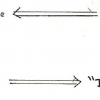
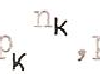
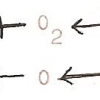



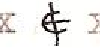

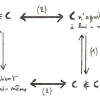

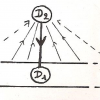

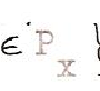
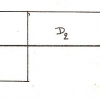


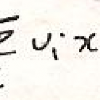
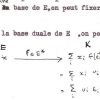
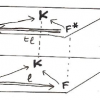

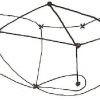
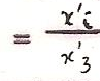

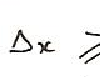



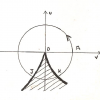




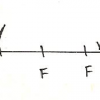

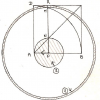


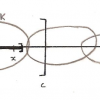




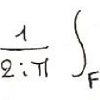

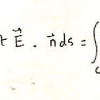
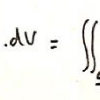


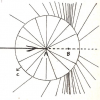
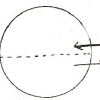
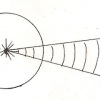

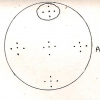
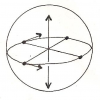
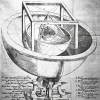
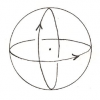
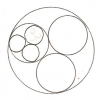



Aucun commentaire to “Les figures de l’Intuition”