Le polyèdre de Melencolia I, invention de Dürer qu’on ne trouve nulle part ailleurs, est une énigme géométrique sophistiquée qui a résisté pendant plus de quatre vingts ans  aux investigations des chercheurs. Nous allons résumer ici l’article probablement définitif de Hans Weizel [1] qui reprend de manière systématique les travaux de ses prédécesseurs (essentiellement allemands) et propose, sur la base d’un croquis de Dürer récemment retrouvé [2], une reconstruction très convaincante de la démarche  intellectuelle suivie par l’artiste.

Ce chapitre risque de décevoir ceux qui privilégient un sens mystique ou ésotérique. Ceux qui s’intéressent  à la genèse complexe des idées et à la reconstruction encore plus complexe de cette genèse, trouveront ici une passionnante page de l’Histoire des Sciences et de l’Histoire de l’Art réunies.

Article précédent : 3 La question de la Sphère

Un cube posé sur sa pointe

Page de titre de  « Instrumentum sinuum sive primi », Petrus Apianus, 1534, Nüremberg

Vingt ans à peine après Melencolia I et dans la ville même de Dürer, un graveur inconnu s’est livré à un exercice de géométrie bien plus approximatif. Le morceau de bravoure réside   dans la table en forme d’étoiles à sept branches (comme les sept planètes), plutôt que dans le cube posé sur sa pointe.

Cette gravure à l’avantage d’illustrer l’interprétation  la  plus simple du polyèdre de Dürer :  un cube dressé selon sa diagonale, puis tronqué en haut et en bas. Elle a aussi l’avantage de montrer les écueils d’une perspective au jugé. Dans un cube, l’angle réel aux sommets de chaque faces est de 90°, tandis que l’angle apparent, du fait de l’inclinaison de la face, est plus grand pour les points haut et bas et plus petit  pour les points gauche et droit. Ici,  le graveur maladroit a mis  un angle droit en bas, ce qui donne cette impression « de guingois ».

Les avantages du cube

Le cube est une forme parfaite, qui complète agréablement la sphère posée juste en dessous.

Cette forme  satisfait donc toute une série de chercheurs :  Nagel (1922), de Haas (1951), Wangart, (1968, 1976), Strauss (1972a, 1974), Bashir-Hecht (1985).

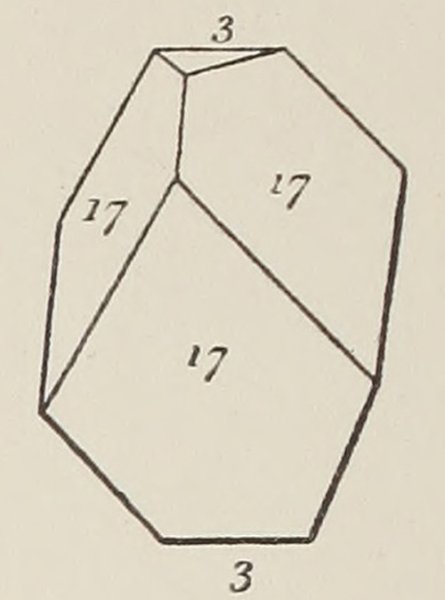
Un cristal, mais lequel ?

Cristal de calcite, Atlas der Krystallformen (1913)

Grodzinski (1955) fait des essais avec des modèles en papier pour trois angles  : 60 ° (octaédre), 72 ° (rapport d’or) et 90 ° (cube), persuadé que le polyèdre représente un diamant, qui cristallise soit sous forme d’octaèdre, soit sous forme de cube. Surprise :  le modèle qui s’accorde le mieux avec le polyèdre de la gravure est celui de 72°.

Néanmoins Steck (1958) persiste sur l’octaèdre et le diamant.

Roesch (1970) reprend les modèles de Grodzinski en essayant un angle supplémentaire, 102° (celui de la calcite), et confirme que le meilleur accord est bien avec l’angle de 72°. MacGillarty (1982) propose-elle aussi un cristal de calcite, mais d’angle 79°+_1.

Grigoriev et Schafranovsky (1973)  proposent un cristal de fluorine, métal utilisé par les orfèvres comme fondant du temps de Dürer, ce qui a l’avantage d’établir un lien avec le creuset. Mais son angle de 76° est très rare dans la nature (l’angle normal étant de 102°) et rien ne prouve que Dürer ait pu connaître ce type très particulier de cristallisation.

Lynch (1982)  propose 81,8°. La même année, Schall à la suite d’une reconstruction perspective très précise, trouve 79,2°.

A partir de là, la cause du rhomboèdre intermédiaire entre l’octaèdre et le cube est quasiment entendue.

MacKinnon (1993)  tente un dernier compromis pour sauver le cube, en suggérant une sorte d’anamorphose : vu du coin en bas à gauche, le rhomboèdre tronqué devient un cube tronqué.

Plus grand monde ne croit à la représentation d’un cristal naturel :  une dernière tentative  isolée de J.Bordehore (2006), propose  un cristal d’alunite [3]

Désormais, on recherche plutôt une justification géométrique

à cet étrange angle intermédiaire entre le cube et l’octaèdre.

L’angle de 72°

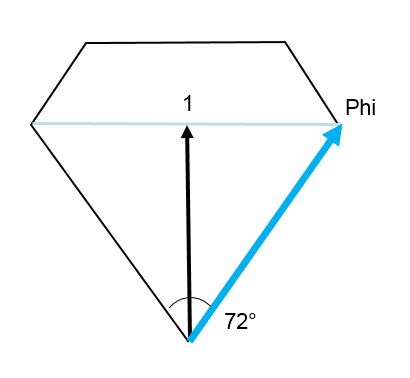
Cet angle, qui est l’angle interne du pentagone,  est très séduisant car il repose sur le nombre d’or ; c’est pourquoi Grodzinski l’avait essayé en 1955, et l’avait retenu comme meilleur candidat à l’issue de ses expériences.

En 1999, Schreiber donne un argument complémentaire apparemment irrésistible : avec l’angle de 72°, en le tronquant au bon niveau, le polyèdre s’inscrit parfaitement  dans une sphère englobante [4].

A partir de là, la messe semble dite, du moins sur le Net  : on trouvera abondamment, en commençant par Wikipedia [4] des constructions géométriques  [5] et symboliques [6], voire des maquettes en papier [7] permettant de construire le « polyèdre de Dürer » avec son angle de 72°.

Seuls grains de sable, régulièrement ignorés :

• n’importe quel rhomboèdre s’inscrit dans une sphère, à condition de le tronquer au bon niveau ;
• Dürer, qui connaissait bien entendu le nombre d’or, n’en a jamais parlé dans ses écrits ; en revanche, il était un grand spécialiste de la géométrie en trois dimension, et notamment d’une famille particulière de volumes  : les polyèdres archimédiens, dont il a étudié, découvert et construit plusieurs. On peut donc s’attendre de sa part, s’agissant  d’un de ses sujets d’étude favoris, à une construction bien plus travaillée qu’un simple jeu sur le nombre d’or ;
• enfin, le polyèdre qui correspond le mieux à celui de la gravure possède un angle particulièrement ingrat (environ 80° ) qui ne correspond numériquement à rien.

Avant de proposer une solution plus satisfaisante, il nous faut comprendre pourquoi tant de chercheurs éminents ont pataugé pendant plus d’un siècle [10], et pourquoi il est si difficile de reconstituer la géométrie précise de ce polyèdre.

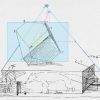
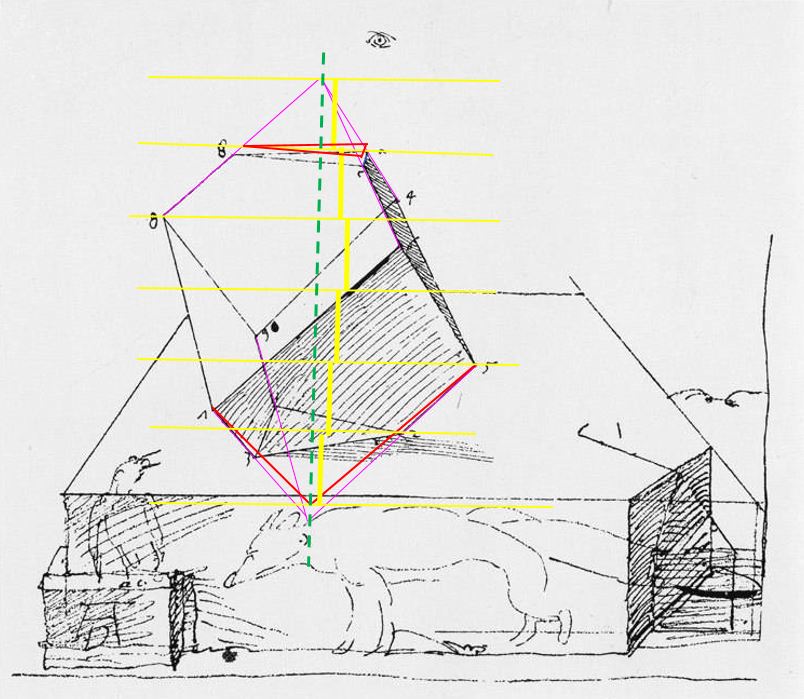
L’esquisse de Dresde

Dürer, dessin à la plume, 1514
Dresden, Sächsische Landesbibliothek

Il ne faut pas s’épuiser à chercher une signification au renard et à l’oiseau à peine esquissés sur le socle : le dessin de la pièce en haut à droite, sans rapport avec la construction géométrique montre seulement le souci d’économiser le papier.

Tous les chercheurs se sont penché avec espoir sur ce précieux croquis qui, en plus de marquer par un oeil la position du point de fuite, dévoile les faces cachées.

Malheureusement, il ne s’agit que d’une étude, donc sujette à imprécisions. Ainsi les lignes qui joignent les points opposés (en jaune) ne permettent pas de définir précisément le centre, et donc la position des axes vertical et horizontal (pointillés blancs). Pour ce dernier axe, on peut considérer qu’il est indiqué par le bord arrière du socle.

Les hypothèses de travail

Mais le problème principal, avec une forme  non régulière comme celle-ci, est que, même connaissant le point de fuite, il n’est pas possible à partir de la seule vue en perspective de déterminer sans ambiguïté sa forme et ses dimensions. Pour y parvenir, voici les hypothèses complémentaires, de bon sens,  que se sont données Schuritz (1919) et Schaal (1982)  (cf [1] Weitzel 2009, p 164) :

• le polyèdre a des faces parallèles deux à deux ;
• il a un axe vertical, et cet axe  est perpendiculaire à l’horizon dans la gravure ;
• les 6 faces latérales ont la même forme ;
• la troncature  est symétrique en haut et en bas, et perpendiculaire à l’axe vertical ;
• les deux triangles équilatéraux ainsi produits à la tête et la base sont égaux ;
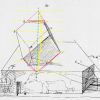
• le polyèdre est tourné de sorte que la pointe droite du triangle du bas et la pointe gauche du triangle du haut soient dans un plan parallèle au plan de l’image (plan bleu sur le schéma).  Ce qui revient à dire que chaque triangle a un côté perpendiculaire au plan de l’image ; et que donc ces deux côtés, ainsi que les diagonales des surfaces latérales, sont des lignes de fuite (en violet sur le schéma). On constate que sur l’étude, ces lignes vont vers un point de fuite qui ne coïncide pas exactement avec celui indiqué par les fuyantes du socle.

Les imprécisions de l’étude

Plus ennuyeux : si on prolonge les côtés pour retrouver la forme du polyèdre avant troncature, on se heurte à d’autres inconsistances :

• l’axe n’est pas exactement vertical ;
• le polyèdre n’est pas exactement symétrique entre le haut et le bas : le triangle supérieur devrait être un peu plus haut ; le triangle inférieur devrait être un peu plus court (lignes rouges).

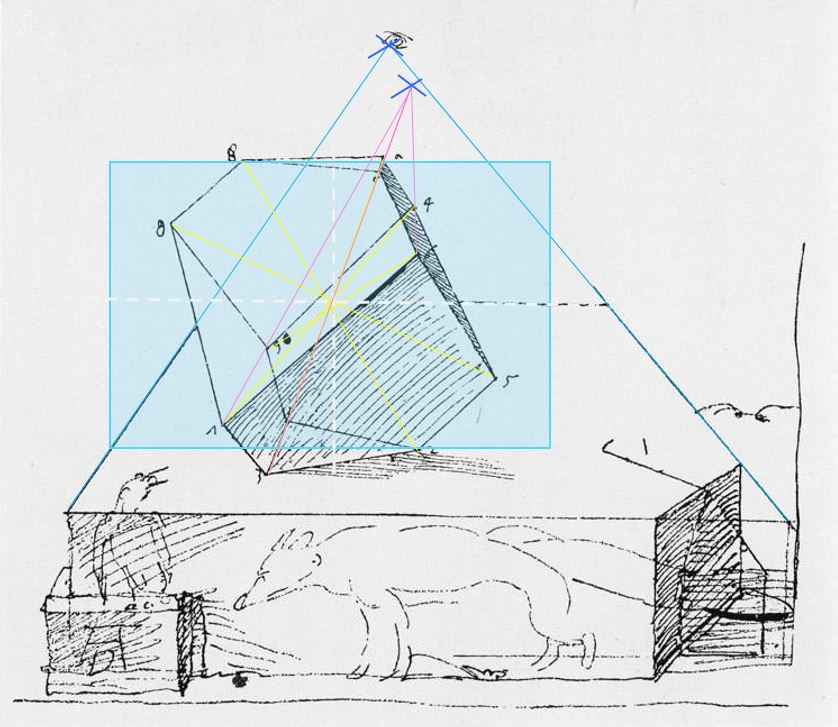
Le polyèdre dans la gravure

Heureusement, toutes ces imperfections ont été corrigées dans la gravure :

• le point de fuite indiqué par la corniche coïncide  avec celui du polyèdre (lignes bleu) ;
• l’axe est vraiment perpendiculaire à l’horizon (pointillé vert) ;
• les deux lignes qui joignent des points opposés se croisent bien sur l’axe (lignes violettes) ;
• il n’y a plus d’anomalie sur les triangles haut et bas.

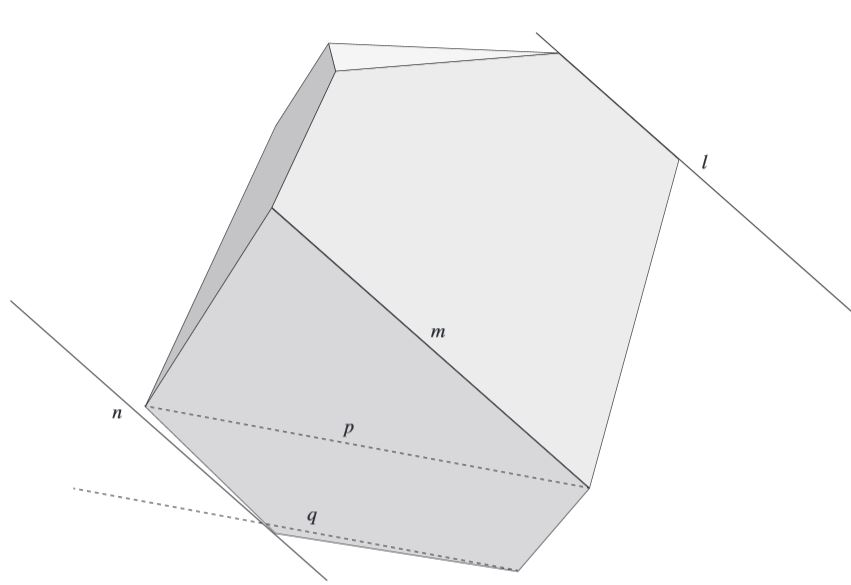
Extrait de Party Game for a 500th Anniversary »,2014 [10]

Il reste néanmoins quelques anomalies très mineures, qui montrent à quel niveau de précision en sont arrivés les polyédristes les plus méticuleux :

• la droite n devrait être parallèle à m et l
• les deux droites p et q convergent faiblement vers la droite, alors qu’elles devraient converger faiblement vers la gauche.

Ceci n’empêche pas  des  reconstructions perspectives très précises, comme celles de MacGillavry (1981)  (79° +-1) et  sutout de Schaal (1982)  , qui en a déduit l’angle très énigmatique de 79,2°.

Attention Scoop ! Ce qui  suit n’a à ma connaissance jamais été expliqué.

L’affinité entre polyèdre et échelle

Le fait de rajouter au rhomboèdre tronqué les deux pyramides qui lui manquent faut apparaître une évidence : le solide complet est un objet composé de six tranches horizontales, exactement  comme l’échelle (horizontales jaunes et bleues).

Le 3ème barreau de l’échelle  coïncide avec le triangle du haut, tandis que le 4ème coïncide avec le point haut du rhomboèdre complet : le pas de l’échelle indique précisément la hauteur de la pyramide à supprimer. Par ailleurs  nous avons vu (voir Question de la Sphère) que ce pas est égal au rayon de la Sphère.

Plus qu’une proximité, l’échelle et le polyèdre affichent une véritable affinité,

qui s’expliquera  par ailleurs  (voir Harmonies polyédriques).

Vue d’ensemble des rapports numériques

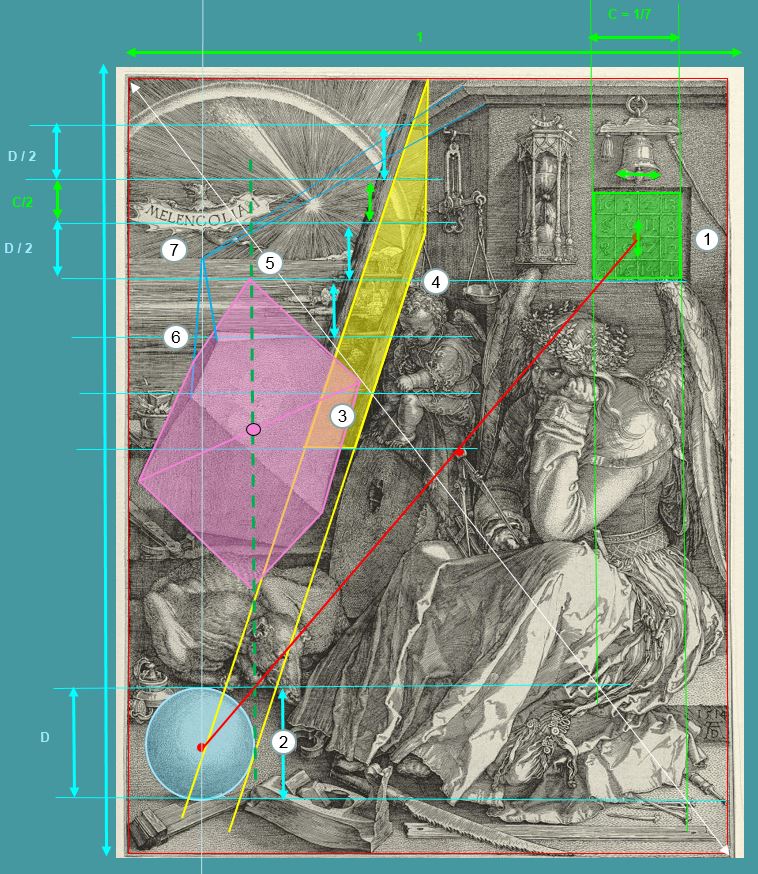
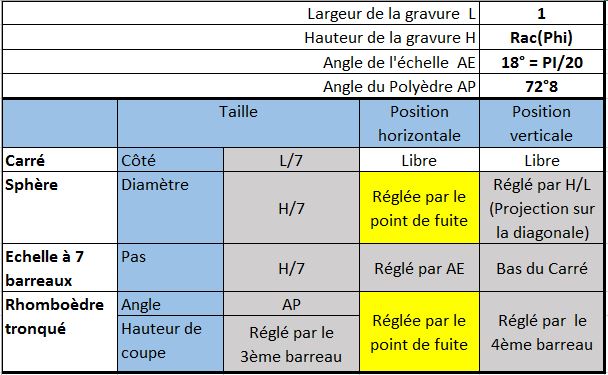
En rassemblant de que nous avons découvert dans Question de la Sphère, et ce que nous venons de trouver à propos du polyèdre, nous pouvons proposer une vue d’ensemble des rapports numériques, finalement assez simples, qui régissent le positionnement et la taille des quatre objets de la Géométrie  : le Carré , puis la Sphère,  puis l’Echelle et enfin le Polyèdre.

• 1) Partons du Carré, dont le côté C vaut 1/7 de la largeur de la gravure.
• 2) En abaissant ses côtés sur la diagonale, nous obtenons le Diamètre D de la Sphère (1/7 de la hauteur de la gravure), et son positionnement vertical. Son positionnement horizontal est donné par la verticale du point de fuite.
• 3) Une fois la Sphère placée, en choisissant l’angle de 18°, nous traçons les montants de l’échelle (en jaune)
• 4) Nous positionnons le barreau central au niveau du bas du Carré, puis les autres barreaux en les espaçant de D/2 (sauf  le 5 et le 6, qui sont espacés de C/2)
• 5) Sur la même horizontale que le barreau central, nous positionnons le coin haut du polyèdre (avant découpe)
• 6)  La position du 3ème barreau  nous donne le plan de coupe, et donc la taille du polyèdre
• 7) Nous ajustons latéralement le polyèdre pour que son point de fuite coïncide avec celui des moulures (c’est pourquoi son axe vertical ne coïncide pas avec le point remarquable que constitue le centre de l’arc en ciel)

Ainsi  les quatre  objets géométriques sont liés entre eux en  taille en position, avec un certain nombre de variables ajustables.

En supposant que Dürer a d’abord choisi des valeurs remarquables pour les  quatre données du haut (l’angle du polyèdre sera expliqué plus loin), neuf des treize variables de positionnement et de taille  des objets sont fixées, et il en reste quatre qui peuvent être ajustées librement : la position du centre du carré et la position du point de fuite.

Le géomètre s’est donné des contraintes  fortes, mais pas inhumaines.

Article suivant : La question du Polyèdre : 4.2 Sa logique

Revenir au menu : 4 Dürer