Se focaliser sur la question de l’angle conduit, comme nous l’avons vu,  à une impasse. Une autre voie consiste  à essayer de retrouver les contraintes internes que Dürer a pu se donner, et donc la  logique interne ce ce polyèdre qui, avec le carré magique, constitue l’objet le plus intrigant de la gravure.

Nous allons poursuivre la lecture de l’article, passionnant comme un roman policier, où Weitzel explique sa découverte et reconstitue la démarche intellectuelle de Dürer [1].

Article précédent : 4.1 Son angle

De nombreux auteurs ont trouvé un lien logique très convainquant entre le polyèdre, le carré magique et, pourquoi pas l’ardoise carrée de l’angelot :

« Dürer n’a-t’il  pas  fait tourner le polyèdre autour de son axe vertical, de manière à ce que l’angelot, assis à cet emplacement remarquable, regarde  dans la direction du rhomboèdre qui montre justement la vue de côté déjà décrite ? Qu’ écrit-il ou  dessine-t-il sur son ardoise, qu’il  cache au  spectateur avec le bras et la main qui tient l’ardoise ? Comment sait-on qu’il s’agit bien de gribouillages ? N’est-ce pas un indice que Dürer  donne au spectateur : Regardez le polyèdre sous la même  direction que le l’angelot, et vous avez résolu l’un des mystères, peut-être Le mystère de l’image ? » Weitzel 2007, p 148

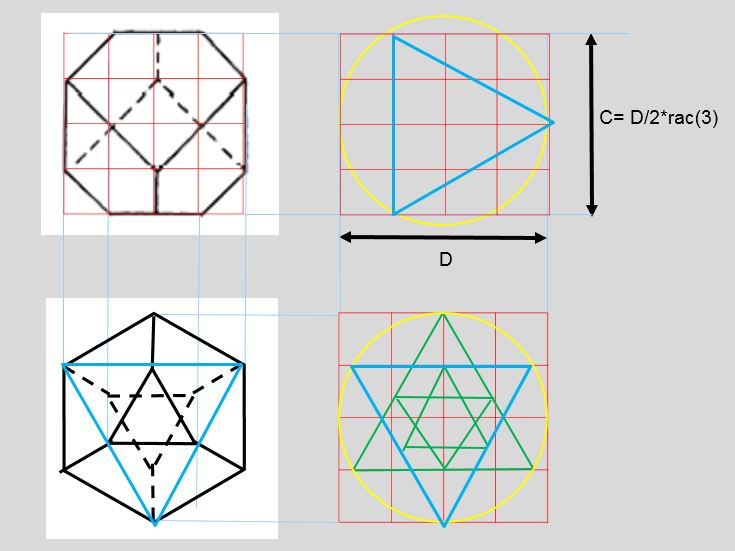
Quel est le mystère que résout cette vue de côté ?  Tout simplement, que le polyèdre vu de côté s’ajuste parfaitement dans un quadrillage carré 4 X 4.

A noter (chose moins souvent remarquée) que la vue de dessous s’inscrit également dans un quadrillage carré 4X4, mais un peu plus grand. Vue de dessous qui fait  apparaître, à l’intérieur d’un hexagone, deux étoiles à six branches imbriquées.

Cette double inscription du  polyèdre dans un quadrillage 4×4 a peut être une signification symbolique. Si le polyèdre (imparfait) a partie liée avec l’astre (erratique) sous l’égide de Saturne, son inscription dans le talisman de Jupiter montre que ce dernier est capable de contrôler Saturne, de l’enfermer dans son épure.

Dans le chapitre précédent ( 4.1 Son angle ), nous avions donné une première contrainte pouvant déterminer la hauteur de la coupe : faire en sorte que tous les sommets du rhomboèdre s’inscrivent dans une sphère (Schreiber, 1999)

Nous avons maintenant une seconde excellente contrainte : faire en sorte que la vue de côté s’inscrive dans un quadrillage 4×4.

Depuis les années 1980, les chercheurs se sont répartis en trois groupes : les tenants de la première contrainte, ceux de la seconde, et ceux de la combinaison des deux.



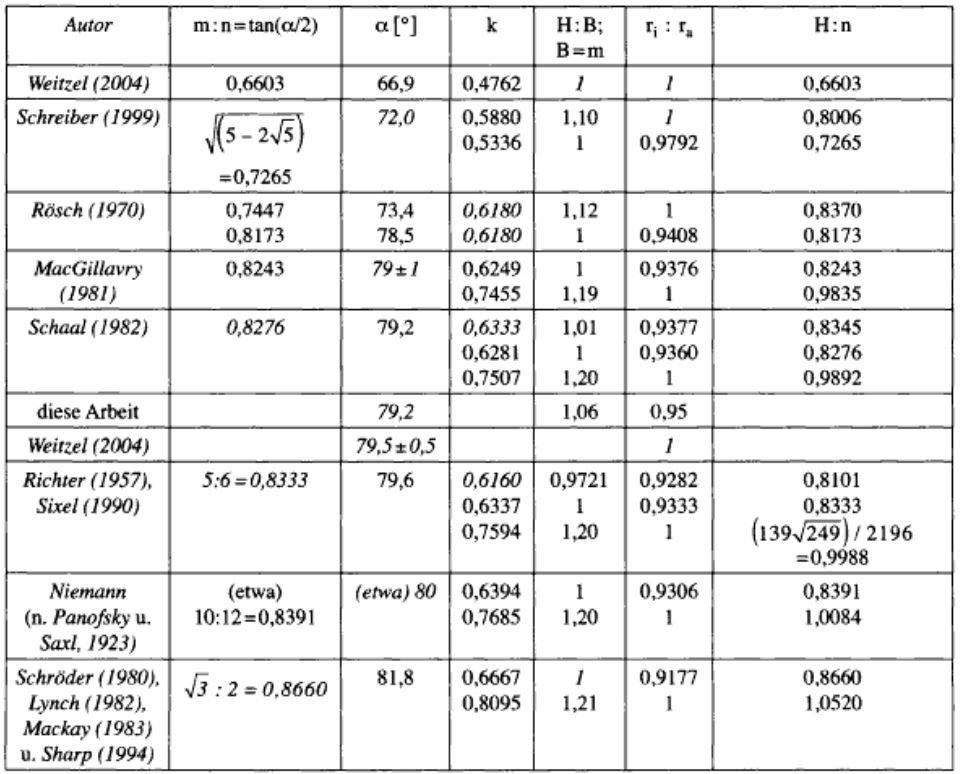
Weitzel, 2007, p 152

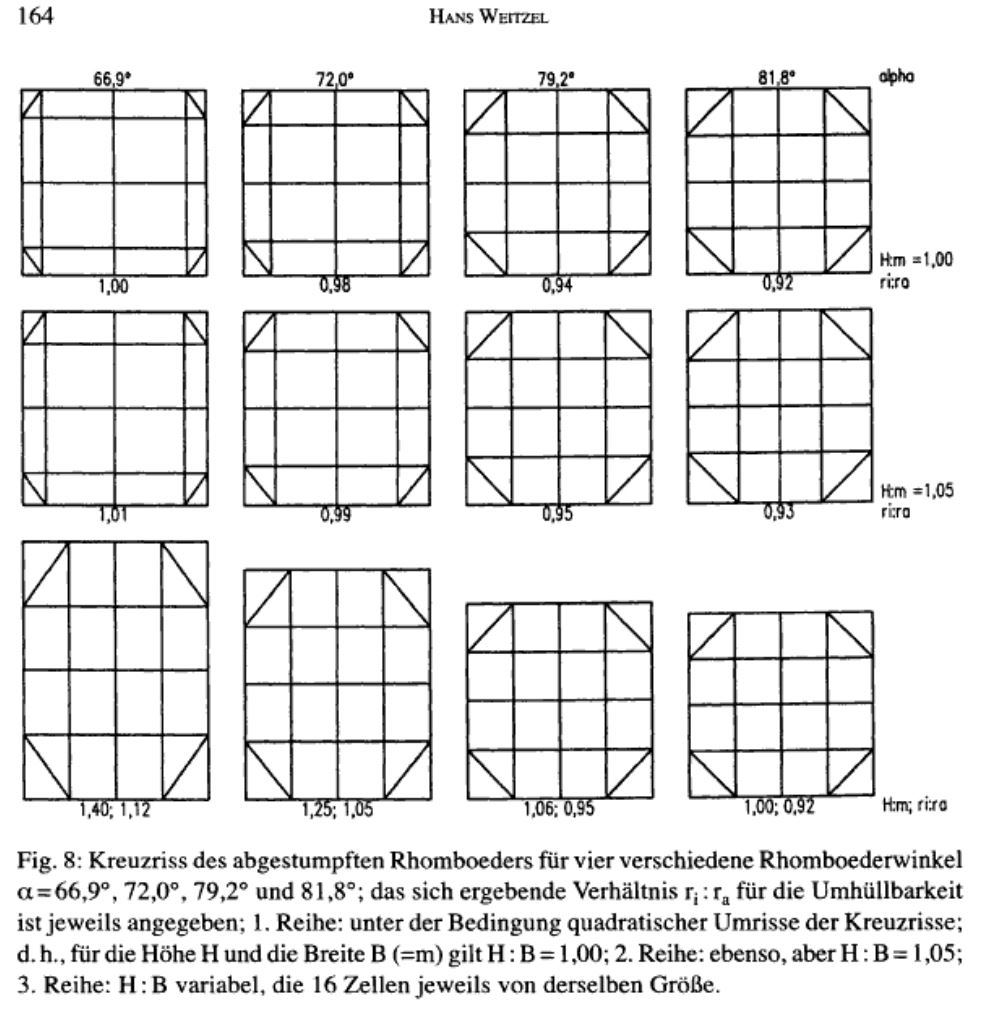
Ce tableau dressé par Weitzel récapitule tous ces efforts : la troisième colonne indique l’angle du polyèdre, la quatrième est le facteur de coupe. Les deux colonnes les plus intéressantes sont les deux suivantes :

• H/B est le rapport entre la hauteur et la largeur de la vue de côté : 1 signifie qu’il s’agit d’un carré
• ri/ra est le rapport entre la sphère interne (passant par les 6 points intermédiaires) et la sphère externe (passant par les 6 points des faces triangulaires : 1 signifie que ces deux sphères n’en font qu’une.

Un rapide parcours permet de voir qu’il y a une seule solution satisfaisant ces deux contraintes (première ligne du tableau) : malheureusement, ce n’est pas celle que Dürer a choisi, puisqu’elle donnerait un angle de 66,9°, vraiment trop loin des 79,2° de Schaal  (la meilleure reconstruction perspective).

Partant de là, Weitzel fait un raisonnement d’ingénieur. Acceptons l’angle de 79°2, et voyons comment Dürer, constatant que les deux contraintes n’était pas compatibles pour cet angle, aurait pu construire un compromis permettant de les satisfaire à peu près.

Weitzel, 2007, p 152

Après étude numérique, le meilleur compromis est la troisième image de la troisième ligne (5% d’erreur sur chaque condition)

La découverte de Weitzel

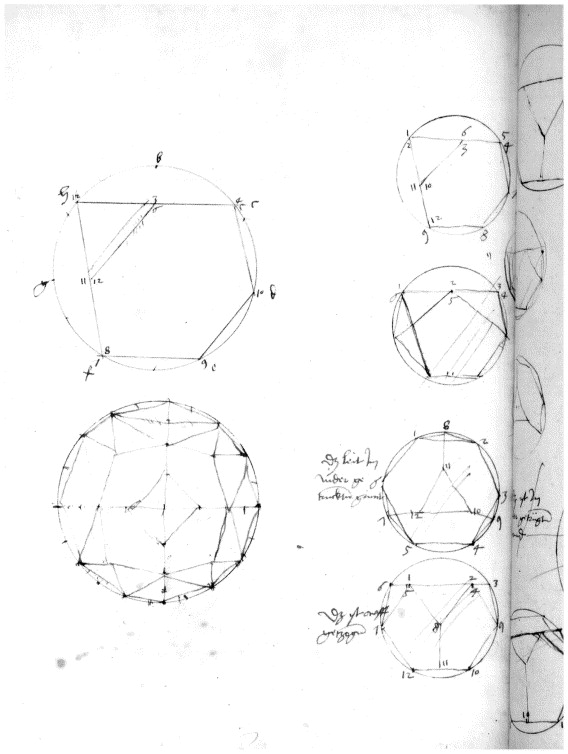
Feuille 127v, Durer Bandes, Nurnberger Stadtbibliothek

En 2004, Weitzel compulse les croquis laissés par Dürer lors de ses recherches sur les polyèdres archimédiens, vers 1510. Voici comment il décrit cette page dans son article [2] :

Dans la colonne de droite, de bas en haut,  le premier  « semble être une tentative de construire un solide d’Archimède (3,5,5), qui ne peut  pas exister. Comme Dürer a écrit, « Daz ist awff getzogen » : il est montré en élévation. » (remarque : la notation 3,3,5 indique que chaque sommet réunit un triangle et deux pentagones) « Le suivant, à savoir, le solide d’Archimède (3,6,6), est présenté en vue de dessous, et en conséquence Dürer a écrit, « Daz leit jm Nider grognement getruckten» (transcriptions par Rupprich [1969]). Le suivant semble le solide d’Archimède (3,5,3,5). Enfin, le croquis en haut n’est pas un solide, mais le pentagone irrégulier de Melencolia I. Cette esquisse ne contient que des lignes qui existent aussi dans l’esquisse du solide (3,5,3,5) en dessous. Nous pouvons ainsi voir, comment Dürer a développé les grandes lignes du pentagone à partir de ce solide d’Archimède. Son intention était de construire le solide d’Archimède (3,5,5); le résultat a été le polyèdre de Melencolia I. »

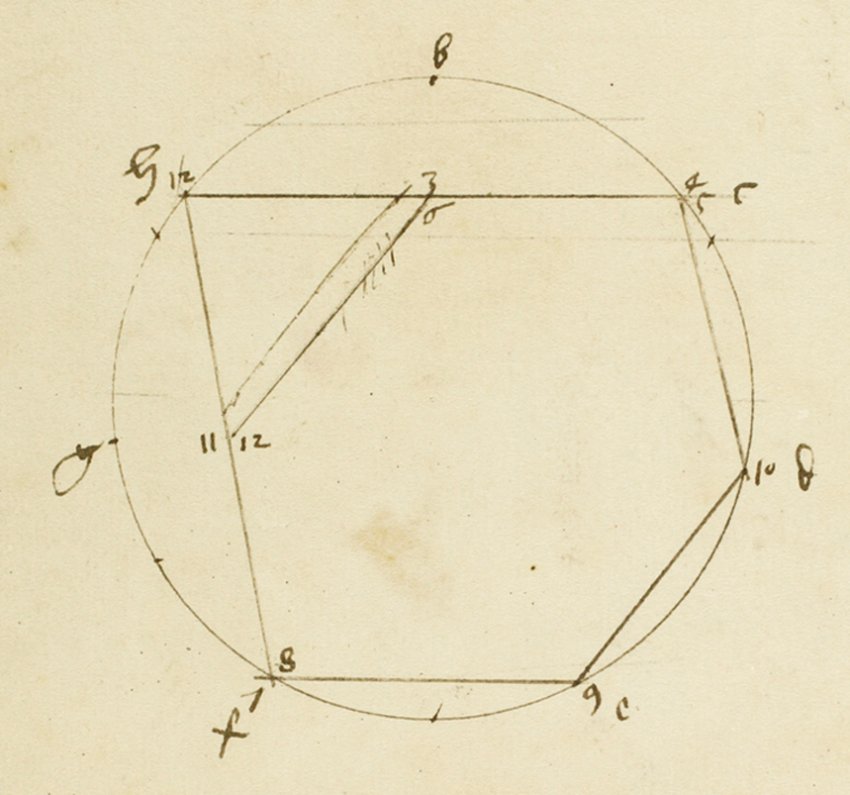
Le croquis en haut à gauche reprend à la règle et au compas l’esquisse sommaire du haut de la colonne de droite. En mesurant l’angle, on trouve 79,5°+-0,5, en parfait accord avec la valeur de Schaal.
De plus, les cinq sommets de cet polygone sont inscrits dans un cercle. Or, cette condition dans le plan se traduit par une condition équivalente dans l’espace :

« On peut montrer que pour alpha> 60°, la condition de l’existence d’un cercle englobant le rhombe tronqué, est interchangeable avec la condition introduite par Schreiber (1999), d’une sphère englobant le rhomboèdre tronqué de Melencolia l. En d’autres mots :  l’englobement du rhomboèdre tronqué exige des pentagones inscrits dans un cercle,  exactement comme celui du dessin. » Weitzel, p 162

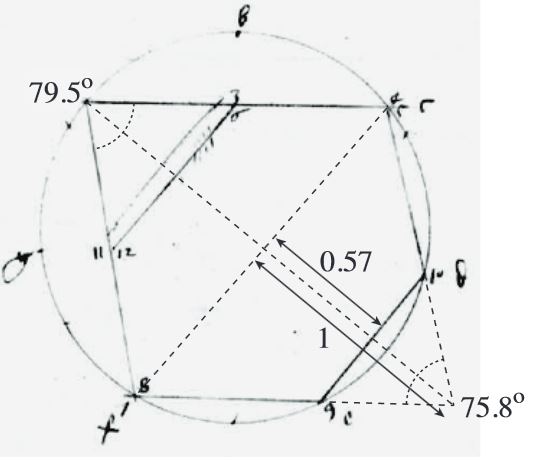
Extrait de « Party Game for a 500th Anniversary »,2014 [3]

Pour être parfaitement honnête, ce pentagone ne représente pas exactement une des faces du rhomboèdre tronqué de Melencolia I, car l’angle opposé est beaucoup plus faible.

Néanmoins, l’étude de Weitzel donne une sacrément bonne intrigue  :

• dans les années 1510, Dürer aurait échoué à construire le solide archimédien [3,5,5], avec un angle de 79,5° ;
• en 1514, en mémoire de cette recherche infructueuse,  il aurait choisi le même angle pour son polyèdre déceptif ;
• il aurait ensuite optimisé la hauteur de coupe, pour trouver un compromis entre deux contraintes inconciliables : autre recherche déceptive.

A la vieille intuition de Panofsky : « Elle (la Mélancolie » ne s’obstine pas sur un objet qui n’existe pas, mais sur un problème qui ne peut être résolu » , Weitzel répond que la gravure illustre bien une double obstination : sur un corps archimédien impossible, et sur un problème sans solution autre qu’une approximation.

Pour conclure ce résumé de la découverte de Weizel,  laissons-lui  la parole, à propos de l’attitude découragée de l’Ange (tandis que l’Angelot gratte encore) :

« Certainement, elle a terminé son travail – mais elle n’est pas pleinement  satisfaite. Mathématiquement parlant : elle aurait voulu obtenir à la fois l’inscription exacte de la vue de côté dans un carré, et  du volume dans la sphère, ce qui suppose que Dürer aussi aurait pu la construire exactement  à la règle et et au compas… » [1], p 168

Scoop !  Pour confirmer que la correspondance entre le carré magique et le polyèdre est  bien un des sujets majeurs  de la gravure, voici quelques considérations complémentaires, qui n’ont jamais été présentées jusqu’ici.

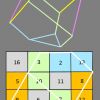
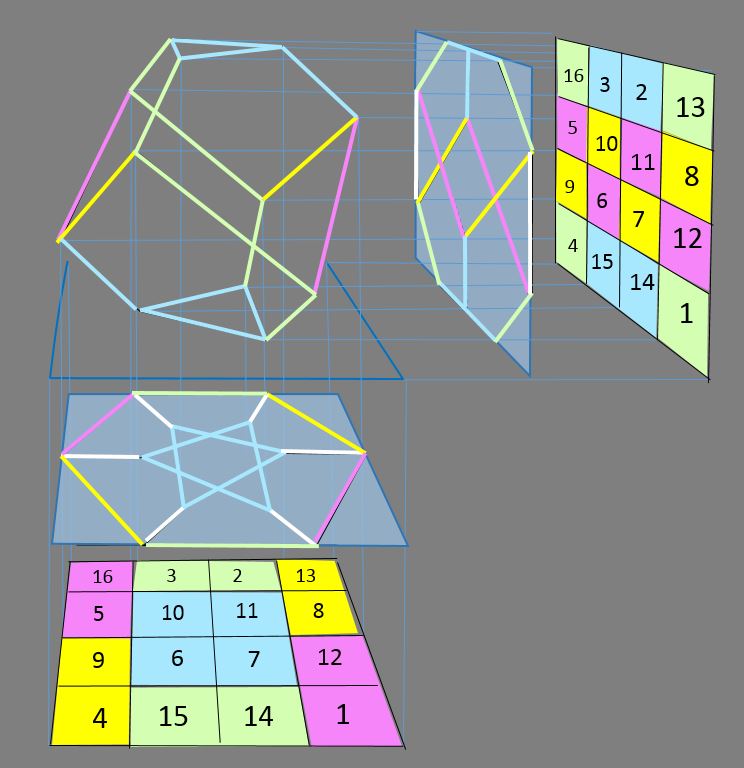
En coloriant  à droite quatre zones de somme 34, on colorie par projection 12 des 14 arêtes de la vue de côté (deux arêtes à cheval entre deux zones restent en blanc).

De même, en coloriant d’une autre manière les cases du carré du carré du bas, on colorie 12 des 18 arêtes de la vue de dessous (six restent en blanc).

Les deux coloriages se combinent pour que, dans la vue en volume, chaque arête ait une couleur unique. Les 16 nombres du carré ne peuvent  numéroter les 18 arêtes du polyèdre : mais  4 zones de somme 34 peuvent, à la manière d’un vitrail, projeter sur chaque arête une couleur unique.  

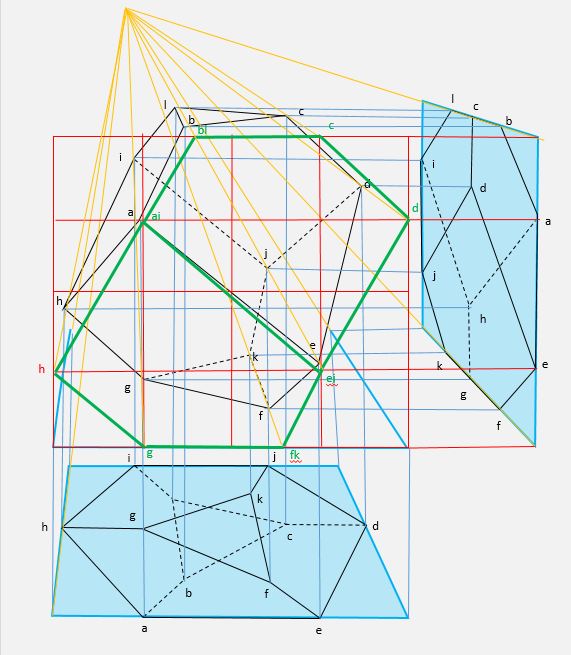
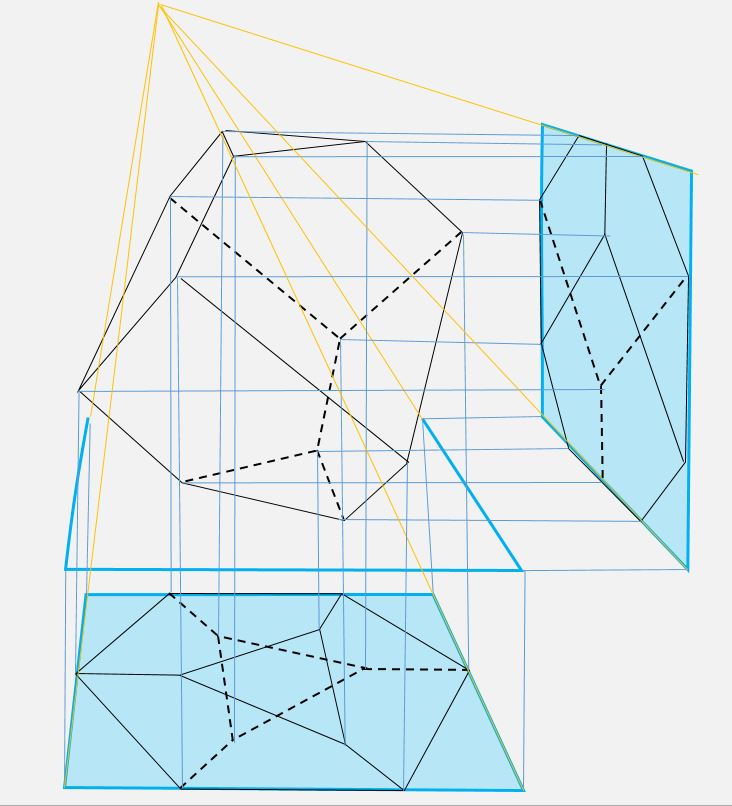
A ce stade, il est logique de construire la troisième projection, vue de face. Elle s’inscrit dans un quadrillage rectangle 4 X 4 (puisque, comme nous l’avons vu, les deux carrés de côté et de dessous ont des tailles différentes). Allons-nous pouvoir colorier ce rectangle de manière cohérente avec les résultats précédents ?

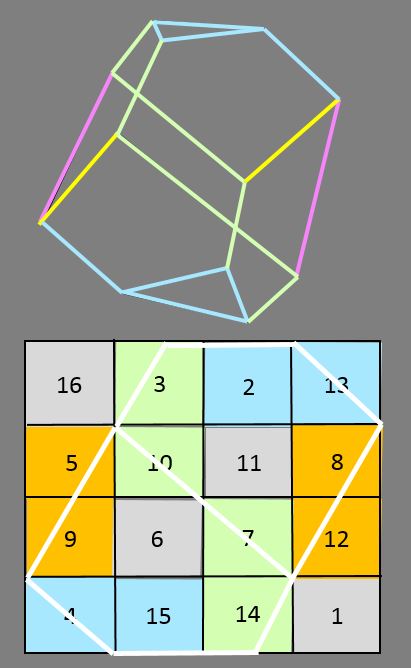
La réponse est oui : les arêtes vert et bleu se projettent dans les cases vert et bleu. Il nous faut une nouvelle couleur (orange)  pour désigner les cases dans lesquelles se superposent des arêtes de couleurs différentes (jaune et cyan). Et une dernière couleur (gris) pour désigner les quatre cases qui ne contiennent aucune arête.

A partir du carré magique, on pourrait écrire un livre donnant, en quadrichromie, tous les coloriages possibles des zones de somme 34 : autrement dit toutes les symétries du carré.

Le mystère que l’angelot griffonne sur son ardoise cachée, c’est que ce livre contient, parmi ses nombreuses pages, les trois projections permettant de construire le polyèdre dans l’espace.

Correspondance proprement stupéfiante entre arithmétique et géométrie : certaines symétries entre les nombres correspondent à certaines symétries entre les arêtes :

le carré magique contient les trois plans du polyèdre.

Article suivant : La question du Polyèdre  :  4.3 La Transformation de Dürer

Revenir au menu : 4 Dürer